Current Divider Calculator

Looking for an all-in-one current divider calculator to estimate the current flowing through each branch of a resistive, inductive, or capacitive circuit? You're in the right place. Let's quickly inform you what our tool can do:

• It's a current branch calculator.
• Explains the current divider rule and how current divides in a resistive circuit with an example.
• Guides you on how to derive the current divider formula for resistive circuits, inductive circuits, and capacitive circuits.
• Helps you understand how other components influence the current flowing through a component in a parallel circuit.

In a nutshell, our tool is a comprehensive current division calculator!

Any circuit that divides current into various paths is a current divider circuit. The magnitude of current passing through a particular path depends on the impedance of that path. Unlike what we saw in the voltage divider calculator, current and impedance have an inverse relationship – the more the impedance of a path, the lesser the current passing through it.

For example, in a parallel connection of two resistors of equal resistance, the current from the source divides equally and flows through each resistor.

Let's take a look at how current divides in a resistive circuit, inductive circuit, and capacitive circuit.

When we connect two components providing parallel resistance (or impedance in AC circuits), the current in any branch is a fraction of the total current. For example, in a 1-ampere DC parallel circuit with a 1Ω-resistor in each of the two branches, the current flowing through the branches is 0.5 A.

As we saw in the Ohm's law calculator, in a parallel resistive circuit, the current flowing through a path is:

where $V$ is the voltage across the path, and $R_\text{path}$ is the effective resistance of the path.

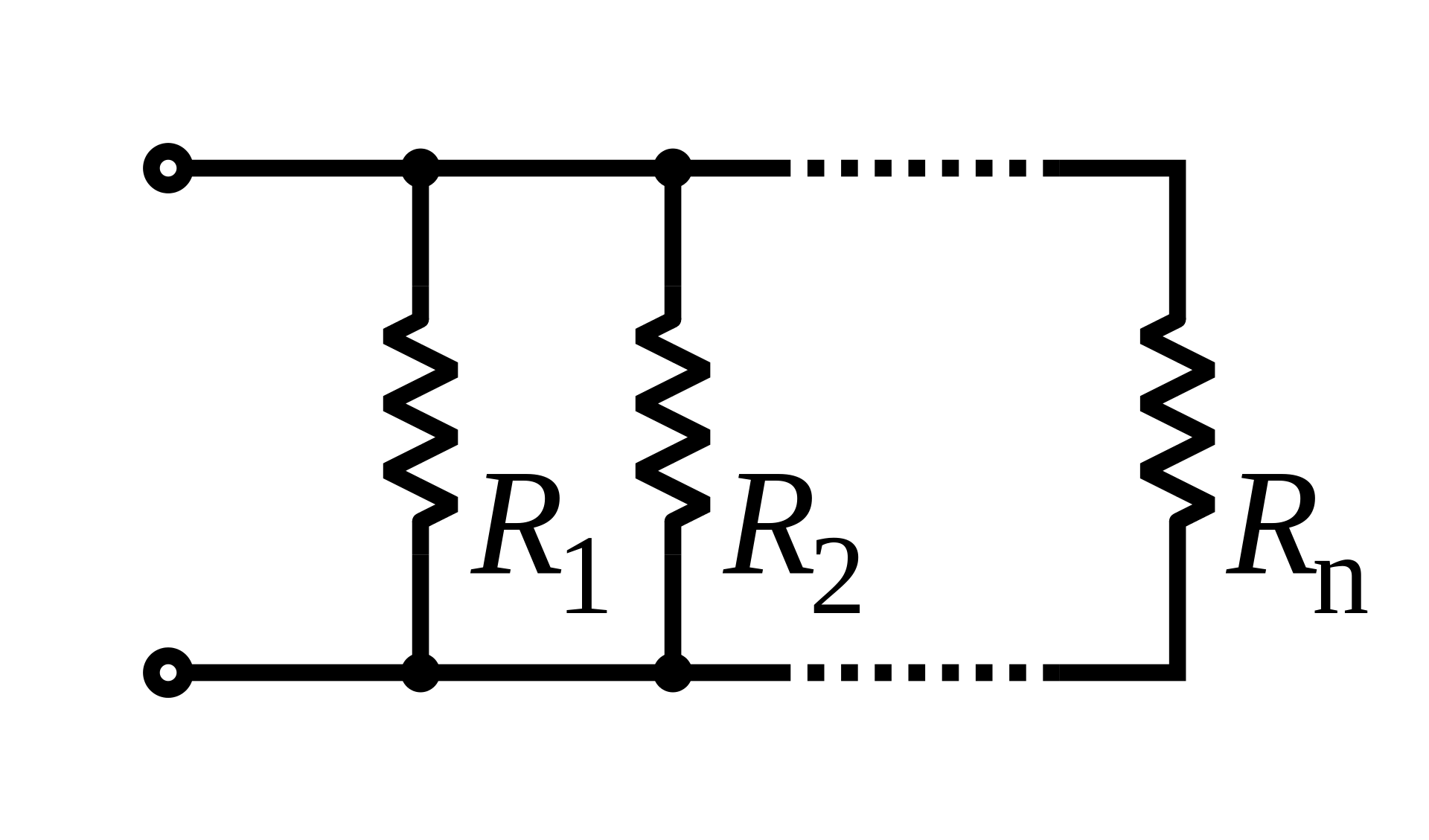
In any parallel circuit, the voltage remains the same across two branches, and it is equal to the product of the source current $I$ and the circuit's effective resistance $R_\text{eq}$:

Consider a parallel resistive circuit of two resistors, $R_\text{1}$ and $R_\text{2}$. The effective resistance, $R_\text{eq}$ of the given parallel circuit is:

On rearranging:

(learn more about this in the parallel resistor calculator).

Thus, the voltage across the paths is:

Now, divide the voltage across the first path by its effective resistance to obtain the current divider formula for $R_\text{1}$:

On simplifying:

Similarly, the current divider equation for the resistor $R_\text{2}$ is:

If you want to add more resistors, you can repeat the process, although the formulas may grow big. But don't worry – simply use our current divider calculator, and you'll get the result in a second!

For a parallel inductive circuit, we can consider the current division only in an alternating current (AC). By analogy to the resistive current divider, we can apply Ohm's law to find the average current flowing through an inductance $L$ using the inductive reactance $X_\text{L}$:

where $f$ is the AC signal frequency.

Consider a parallel inductive circuit consisting of two inductors, $L_\text{1}$ and $L_\text{2}$. We calculate the effective inductance $L_\text{eq}$ as follows:

On rearranging:

(learn more about this in the inductors in parallel calculator).

Thus, the voltage across the path is:

Now, divide the voltage across the first path by its reactance to obtain the current flowing through $L_\text{1}$:

Or:

Similarly, the average current passing through the inductor $L_\text{2}$ is:

Similar to the inductive circuit, the current division in a capacitive one is possible with an AC signal. We can use the capacitive reactance, $X_\text{C}$, to express the average current passing through a loop with capacitance $C$ as:

The effective capacitance of a parallel connection is the sum of the individual capacitances:

The voltage across the first branch of the parallel capacitive circuit is:

Now, divide the voltage across the first path by its reactance to obtain the current divider equation for $C_\text{1}$:

And the current passing through $C_\text{2}$ is:

That's all you need to know about formulas. Now let's try to solve some computational examples and learn how to use Omni's current divider calculator.

Imagine we have a four-resistor setup (R₁ = 20 Ω, R₂ = 40 Ω, R₃ = 80 Ω, R₄ = 100 Ω), and we need to know how the current divides into each branch when we arrange them in parallel. Let's say the source current (I) equals 1 A. Here is how our current division calculator works:

1. Select the Resistive circuit type. It's a default option.
2. Enter the current value (1 A).
3. Input the consecutive resistances into the corresponding resistors' fields. The new ones will appear as you type the previous ones.
4. That's all! The current divider calculator does the rest of the job. As a result, you can see a table with your resistors and the approximate values of corresponding currents flowing through each path:
   • I₁ = 0.513 A;
   • I₂ = 0.256 A;
   • I₃ = 0.128 A; and
   • I₄ = 0.103 A.

To calculate the current through a branch of any circuit:

1. Work out the effective resistance (R_eq) of the whole circuit.
2. Estimate the voltage (V) across the branch using Ohm's law: V = IR_eq, where I is the source current.
3. Divide voltage by the branch's resistance to obtain the current passing through it: I = V/R_branch if it is a resistive circuit.

The charge stored in a capacitor is the product of the capacitance and the voltage applied: Q = CV. The electric current is the rate of electric charge: I = Q/t. That's why we multiply the capacitance with the applied voltage to estimate the branch current.

No. The current flows through all components and is the same across all elements in a series circuit. The series circuit is a voltage divider.

You don't need to use the current divider rule for series circuits. In a series circuit, voltage divides across various components, and the same current flows through all of them.