Quaternion Calculator

Welcome to Omni's quaternion calculator, where we'll deal with this mysterious extension of complex numbers: the quaternions. In short, we represent them using four real values, each corresponding to one of the basic unity quaternions: $1$, $\text i$, $\text j$, and $\text k$. To some, they may seem like an artificial creation to make math even more tricky than it already is. To others, they are a useful tool in 3D geometry: mainly to study quaternion rotation. Unfortunately, this doesn't kill the "tricky" part, and, e.g., quaternion multiplication is not a straightforward operation.

But let's not get ahead of ourselves! We begin with where every math topic begins: with an introduction. In our case, it's the quaternion definition.

Quaternions are an extension of complex numbers. They were first introduced by Sir William Hamilton, who used them to describe several properties of the three-dimensional space (for more, see the dedicated section).

However, nowadays, most often, we introduce them from the algebraic point of view. Let's take a look at the formal quaternion definition.

By the above quaternion definition, we see that the space is spanned by four base elements: $1$, $\text i$, $\text j$, and $\text k$. The three letters don't stand for any particular value: they simply denote independent base vectors. Nevertheless, if $\text i$ seems familiar, it well should! In fact, if the coefficients of $\text j$ and $\text k$ (i.e., $c$ and $d$ in the above quaternion definition) are both zero, then we obtain the (well-known) complex numbers! As such, we indeed obtain their extension.

More or less, Hamilton's idea was to have one expression whose individual parts (i.e., the base elements' coefficients) describe the distinct directions in a three-dimensional space. From there, he only needed to introduce operations between these new thingies. On the one hand, we'd like them to satisfy some properties and form a nice algebraic structure. On the other, the operations should be usable and have real-life explanations. After all, quaternions originated from geometry — a very real-life area of mathematics.

Now that we know what a quaternion is, we can go further. The subsequent sections describe the basic rules governing these numbers. Note how Omni's quaternion calculator lets you find all values and objects we mention. For more information on how to use the tool, see the last section.

This one's easy. Recall from the above section that quaternions are spanned by four base elements: $1$, $\text i$, $\text j$, and $\text k$. As such, if we want to add or subtract two such expressions, we do it the same way as in any vector space: move from one base element to the other and add or subtract the respective coefficients of the two quaternions. And since these coefficients are simply real numbers, it boils down to the very basics of mathematics which we learned in primary school.

Plain sailing, wouldn't you say? Such addition satisfies all the reasonable properties: it's associative, commutative, and every quaternion $q$ has its opposite $-q$ such that $q + (-q) = (-q) + q = 0$.

Unfortunately, the story is a bit more difficult for multiplication and even more so for division.

In real and complex numbers, we got used to the distributive property of multiplication over addition, so we'd like to have a similar law here. After all, quaternions are sums of four elements: the real part and the $\text i$, $\text j$, and $\text k$ parts. In other words, we want to have:

And indeed, it is so. However, we now have to explain how quaternity multiplication works on the individual parts, i.e., on the basic unity quaternions. The following table contains the answer:

For completeness, let's write the individual products below:

In particular, we see that quaternion multiplication is not commutative. However, it is associative, which means the quaternion space is not a field (unlike, e.g., the real or complex numbers). Instead, it's a division ring since every non-zero quaternion has an inverse, as we'll see in the next section.

Coming back to the formula for the product of two quaternions, we can now use the rules given above to write:

The operation is often called the Hamilton product in honor of its creator.

Recall from the first section that the idea behind the quaternion definition was for the $4$-tuples to represent the three-dimensional space. A keen eye may observe that if we multiply two quaternions whose real parts are zero (i.e., $a = e = 0$ above), then we get precisely the same formula as that of the cross product of two three-dimensional vectors with $\text i$, $\text j$, and $\text k$ corresponding to the elementary basis $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$, respectively.

As for dividing quaternions, the matter is even more tricky. As you may know, algebraic structures don't have the operation of division, per se. The expression $x / y$ is simply an abbreviation of $x \cdot y ^{-1}$. What is more, in real or complex numbers, we have $x / y = x \cdot y ^{-1} = y^{-1} \cdot x$.

On the other hand, we've already mentioned that quaternion multiplication is not commutative, so in general, $x \cdot y^{-1}$ is not the same as $y^{-1} \cdot x$. Therefore, Omni's quaternion calculator returns both possibilities for the two operations, i.e., $x \cdot y$ and $y \cdot x$ for multiplication, and $x \cdot y^{-1}$ and $y^{-1} \cdot x$ for division.

Either way, division requires finding $y^{-1}$, i.e., the multiplicative inverse of a quaternion. And how do we do that?

The magnitude (or norm), conjugate, inverse, and matrix representation are all assigned to a single quaternion. Below, we explain them one by one.

1. The magnitude (norm) of a quaternion

If the name rings a bell, and you feel there was something similar connected with vectors, you're on the right track. As mentioned in the first section, quaternions are simply $4$-tuples of real numbers: same as vectors of a four-dimensional Euclidean space. Those vectors all had their magnitude, which basically described their length. So why don't we repeat the reasoning here?

Recall that the magnitude of a vector (in whichever dimension) is the square root of the sum of its coordinates' squares. Analogously, the magnitude (or norm) of a quaternion is:

Note how, by definition, the value is always a non-negative real number. What is more, it's equal to zero if and only if the quaternion is zero, i.e., $0 + 0 \cdot \text i + 0 \cdot \text j + 0 \cdot \text k$.

Lastly, observe that if we divide a quaternion by its norm (i.e., divide each of its coefficients), we'll obtain a new quaternion whose magnitude is $1$. This simple fact will become quite useful very soon.

2. The conjugate of a quaternion

Recall how the conjugate of a complex number gave the number with the same real part but the opposite imaginary part. This time, we're dealing with expressions of the form $a + b \cdot \text i + c \cdot \text j + d \cdot \text k$ that have one real part (i.e., $a$) and three non-real ones (i.e., $b$, $c$, and $d$). Nevertheless, the concept stays the same: we keep the first unchanged and flip the signs in the others.

To be precise, the quaternion conjugate formula states that the conjugate of $a + b \cdot \text i + c \cdot \text j + d \cdot \text k$ is $a - b \cdot \text i - c \cdot \text j - d \cdot \text k$.

We denote the conjugate of a quaternion $q$ by $\overline q$ (as above), but some sources also use $q^t$, $\tilde q$, or $q^*$.

Also, observe that if we multiply a quaternion by its conjugate in whichever order, we'll obtain a difference of squares:

If we expand it according to the rules from the above section, we'll get:

Again, a simple fact that will prove very useful.

3. The inverse of a quaternion

Let's begin with the obvious: only non-zero quaternions have an inverse. Secondly, even with quaternion multiplication not being commutative, every non-zero $q$ has its inverse $q^{-1}$ such that $q \cdot q^{-1} = q^{-1} \cdot q = 1$, where $1 = 1 + 0 \cdot \text i + 0 \cdot \text j + 0 \cdot \text k$.

To find the reciprocal, recall that for every quaternion $q$, we have $q \cdot \overline q = \overline q \cdot q = \left\| q \right\| ^2$. For a non-zero $q$, this gives $q \cdot \left( \frac{\overline q}{ \left\| q \right\| ^2}\right) = \left( \frac{\overline q}{ \left\| q \right\| ^2}\right) \cdot q =1$, which means that:

(Note how in the above section, we mentioned some issues with dividing quaternions. However, here, we divide by a positive real number, i.e., divide each of the quaternions coefficients. In other words, everything is fine.)

4. Matrix representation

Complex numbers are pairs of real numbers, and quaternions are $4$-tuples of real numbers. And just as we can represent the prior as $2 \times 2$ matrices, we can have the latter as $4 \times 4$ ones. The matrix representation basically takes the quaternion's coefficients and puts them in the right places with the right signs (which come from the relations between unity quaternions). To be precise, we can write $q = a + b \, \text i + c \, \text j + d \, \text k$ as:

In fact, alternatively, we can also use an equivalent $2 \times 2$ matrix representation with complex entries:

To motivate the concept, let us mention a couple of its properties: the magnitude $\left\| q \right\|$ is equal to the square root of the matrix' determinant, and the conjugate $\overline q$ corresponds to the conjugate transpose.

Alright, we've learned the basic operations, including quaternions, but so far, we've only seen formulas that may seem useless by themselves. Now, it's time for some practical uses! We'll get back to geometry, learn to convert a quaternion to a rotation matrix, and see how it all works in the three-dimensional space.

The three-dimensional Euclidean space consists of points $(x, y, z)$ with arbitrary real numbers as coordinates. If we see it as a vector space, it's spanned by three elements: $(1, 0, 0)$, $(0, 1, 0)$, and $(0, 0, 1)$, which we call the elementary basis. On the other hand, there are four basic unity quaternions: $1$, $\text i$, $\text j$, and $\text k$. However, if we think of the non-real ones as analogous to the elementary euclidean vectors, we can use them for quaternion rotation.

To have rotation, we need an axis around which we rotate and an angle. The prior will simply be a straight line, but for calculations, we don't really need any line equations. In fact, a single non-zero vector will suffice: it uniquely defines a line by setting its direction.

Clearly, we can define a line using many different vectors as long as they are scaled versions of one another. Therefore, for our purposes, we'll stick to unit vectors (i.e., those of length $1$). You can transform any non-zero vector $\vec v$ into a unit one by dividing it (i.e., dividing all its coordinates) by its length: $\vec v / \left | \vec v \right |$. Obviously, we could alter the formulas to allow other vectors, but it's far simpler to write them with this simple assumption. Nevertheless, note that Omni's quaternion calculator allows non-unit ones: it simply converts them itself.

You can read more about vectors at our vector calculator or the unit vector calculator.

Now, let's cover two topics connecting quaternions to rotation, one by one.

1. Rotation around an axis

Suppose a unit vector $\vec v_\text a = (x_\text a, \ y_\text a, \ z_\text a)$ defines a line in a three-dimensional space.

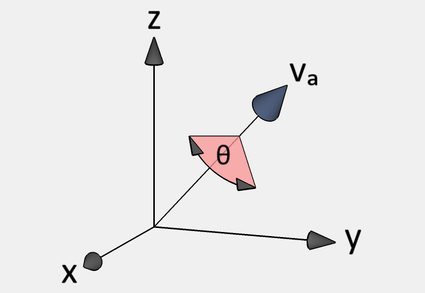
Then, we can represent the rotation around the line by an angle $\theta$ by the quaternion:

Alternatively, we can recall that a three-dimensional space consists of triples of real numbers. Therefore, we can choose to write such triples as matrices with three rows and one column. Then, if we write the $q$ above as $q = a + b \cdot \text i + c \cdot \text j + d \cdot \text k$, we can represent the operation with a $3 \times 3$ matrix, i.e., we can change a quaternion to a rotation matrix given by the following formula (note how this is a very different concept than the matrix representation in the above section):

2. Vector rotation

Point 1. tells us how to "store" the data and the idea of rotating around an axis. Point 2. tells us what we get when we apply the rotation to a given vector $\vec v = (x, \, y, \, z)$.

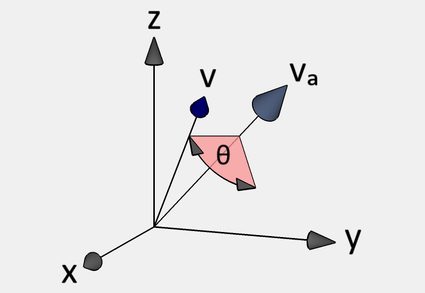
The first option is to use the rotation matrix $R$ above and multiply it by $\vec v$ (represented as a one-column matrix). Then, the vector $\vec v' = R \times \vec v$ is the result of rotating $\vec v$ around the axis given by $v_\text a = (x_\text a, \, y_\text a, \, z_\text a)$ by an angle $θ$.

Alternatively, we can use quaternions and quaternion multiplication. However, before we begin, we need to understand $\vec v$ as a quaternion: after all, right now, it's simply a triple of real numbers.

Define a quaternion $q_\text v = 0 + x \, \text i + y \, \text j + z \, \text k$. In this language, we the rotated vector $\vec v'$ from conjugating $q_\text v$ by the rotation quaternion $q$ from point 1. To be precise, if we set $q_\text v' = q \cdot q_\text v \cdot q^{-1}$, then the result will take the form $q_\text v' = 0 + x' \, \text i + y' \, \text j + z' \, \text k$, and from there we read off the vector: $\vec v' = (x', \, y', \, z')$. In fact, in this case, the rotation quaternion $q$ is unitary (i.e., has magnitude $1$), so $q^{-1} = \overline q$, meaning we could have used the conjugation instead of inverse above.

That concludes the theoretical part. Let's now make good use of the knowledge of what a quaternion is and all the formulas and take on an example or two.

The above sections took us through all the functionalities of Omni's quaternion calculator. Arguably, there are quite a few, so let's try out a couple to get a taste. We'll find:

1. The result of quaternion multiplication of $q_1 = 2 - \text i + 3 \, \text j + \text k$ and $q_2 = 5 - 4 \, \text i + \text k$, and
2. The quaternion of rotation corresponding to the line given by the vector $\vec v_\text a = (1, 0, -1)$ and the angle $θ = 60°$.

Obviously, we'll apply the formulas we've learned. However, before we do that, we let the quaternion calculator do the talking and work out the solution for us.

1. To multiply two quaternions using our tool, we begin by telling the calculator what we want from it. In our case, this means choosing "product" from the list in the variable field "I want to find the…" That will trigger two sections underneath, each dedicated to one of the quaternions. Note how at the top of them, we can see the symbolic representation that is used below: $q_1 = a + b \, \text i + c \, \text j + d \, \text k$ and $q_2 = e + f \, \text i + g \, \text j + h \text \, k$. Looking back at the example, we input:

(Note how we have $b = -1$, $d = 1$, and $h = 1$ even though there were no numbers in the corresponding places in $q_1$ and $q_2$ above. That is because, by convention, we don't write $1$s in front of variables. Also, observe that we input $g = 0$ since $q_2$ has no summand with the unity quaternion $\text j$: that means its coefficient is, in fact, $0$.)

Once we write the last entry, the quaternion calculator will spit out the answer underneath.

2. Again, we begin by stating what we need. This time, we choose "quaternion of rotation" under "I want to find the…" This will trigger two sections: one for the coordinates of the vector defining the rotation axis and one for the angle. The prior is written symbolically as $\vec v_\text a = (x_\text a, \, y_\text a, \, z_\text a)$, and the latter simply by $\theta$. Looking back at the example, we input:

(Note how the tool lets you change the angle unit if needed.) The moment we give the last value, the quaternion calculator presents the answer underneath. Note how apart from the rotation quaternion, it also converts the quaternion to a rotation matrix.

Alright, we've played around a bit; now it's time to get our hands dirty. Surely, we won't be as fast as the calculator, but let's go through the calculations nevertheless.

1. Here, we simply follow the quaternion multiplication rules described in the dedicated section, i.e., use the distributive property of multiplication over addition, and compute the products of basic unity quaternions.

2. To find the quaternion of rotation, we begin by finding the unitary equivalent of the vector $v$. For that, we start with its length:

and use the appropriate formula:

Now, it's enough to use the formula from the dedicated section:

Lastly, if we choose to convert the quaternion to a rotation matrix, the same section provides the formula to do so:

which is:

Phew, that was some work, wouldn't you say? And the sine and cosine were fairly simple, so it can be even longer in general. Oh, it's a good thing we have Omni's quaternion calculator to spare us the hassle!

To use quaternions for rotation, you need to:

1. Identify the vector defining the axis of rotation.

2. If needed, find its unit equivalent.

3. The quaternion of rotation is q = cos(θ/2) + (x_a × i + y_a × j + z_a × k) × sin(θ/2), where:

   • v_a = (x_a, y_a, z_a) is the unit vector defining the axis; and

   • θ is the angle by which you rotate.

4. If needed, rotate v using the formula q_v' = q × q_v × q⁻¹, where:

   • v = (x, y, z) is the vector you rotate;

   • q is as in step 3;

   • q⁻¹ is the multiplicative inverse of q;

   • q_v = x × i + y × j + z × k;

   • if q_v' = 0 + x' × i + y' × j + z' × k, then v' = (x', y', z'); and

   • v' is the result of rotating v.

To multiply quaternions, you need to:

1. Use the distributive property of multiplication over addition.

2. Multiply basic unity quaternions according to the rules:

   • 1 × i = i × 1 = i, 1 × j = j × 1 = j,1 × k = k × 1 = k;

   • i² = j² = k² = -1;

   • i × j = k, j × k = i, k × i = j; and

   • j × i = -k, k × j = -i, i × k = -j.

3. Simplify by combining common summands.

4. Enjoy your quaternion product.

Yes, we can express any rotation around an axis in a three-dimensional space by a unit quaternion. By default, the formulas are for axes going through the origin, but you can always compose the rotation with a translation to suit your purposes.

No. Quaternion multiplication is not commutative, which is a must-have for a structure to be a field. However, all other field properties are satisfied, so, in the end, quaternions form a division ring.

No, or, to be precise, quaternion multiplication isn't commutative. On the other hand, quaternion addition does commute.