a+bi Form Calculator

Welcome to Omni's a+bi form calculator, where you can quickly convert a complex number from its polar to rectangular form. Keep reading if you want to learn or recall what these two forms of a complex number are and how to write the a+bi form of a polar form complex number.

The two forms of complex numbers are: rectangular (a + bi) form and polar (r × exp(φi)) form. The rectangular form describes z as the point (a, b) on a complex plane. The polar form describes z in terms of distance r from (0,0) to z and of the angle φ between the horizontal axis and the radius connecting (0,0) and z.

Let us summarize the two pairs of coordinates:

• a is the real part; and
• b is the imaginary part of z.

And the polar form:

• r is the modulus (or the magnitude)
• φ is the argument of z.

Observe where these value appear in the complex plane:

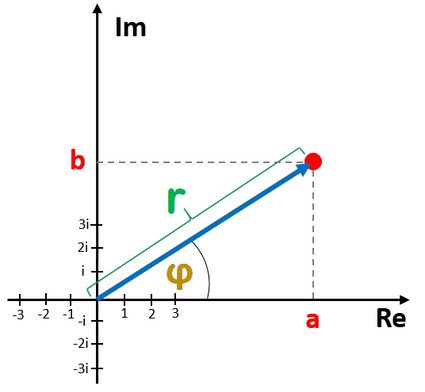
Let us now discuss how to convert the polar form to rectangular form.

When you want to write the a+bi form of a complex number in polar form z = r × exp(iφ) use the formulas:

a = r × cos(φ)

and

b = r × sin(φ).

To see why these formulas are correct, look at the picture above and recall the basic trigonometric formulas:

cos(φ) = a / r

and

sin(φ) = b / r.

Solve for a and b and you'll get the formulas given above.

Omni's a+bi calculator uses the same formulas as well.

Our a+bi calculator is very easy to operate: to convert a polar form to a rectangular form, you need to input the polar form by filling in the fields magnitude and phase. Note that for the phase, you can choose between radians and degrees - pick whatever is more convenient for you!

Our a+bi form calculator immediately displays the two coordinates of the rectangular form: the real part a and the imaginary part b. You can now write the a + bi form easily.

Satisfied with this a+bi form calculator? Omni can help you discover various interesting aspects of complex numbers! Take a look and pick the next thing you want to learn:

• Complex number calculator;
• Multiply complex numbers calculator;
• Divide complex numbers calculator;
• Imaginary number calculator;
• Complex number to polar form calculator;
• Complex number to trigonometric form calculator;
• Complex number to rectangular form calculator;
• i calculator; and
• Polar form calculator.

To convert a complex number from polar to rectangular form:

1. Compute cos(φ) and sin(φ) , where φ is the argument of your number.
2. Multiply each of these two numbers by r, where r is the magnitude (modulus) of your number.
3. The real part of your number is a = r × cos(φ).
4. The imaginary part of your number is b = r × sin(φ).
5. Write the a + bi form of your number.

The answer is √2/2 + (√2/2)i. To derive this result, observe that the modulus of exp(iπ/4) is 1. Next, compute cos(π/4) = √2/2 and sin(π/4) = √2/2. In consequence:

• The real part is a = 1 × cos(π/4) = √2/2.
• The imaginary part is b = 1 × cos(π/4) = √2/2.

If you struggle or want to verify your calculations, don't hesitate to use an online a+bi calculator.