Complex Number to Rectangular Form Calculator

Omni's complex number to rectangular form calculator will help you whenever you're stuck with a complex number in its polar form (the one with exponent, modulus, and argument) and need it quickly converted from this exponential form to rectangular form.

In what follows, we will recall what the rectangular form is all about and what formulas stand behind the conversion from polar to rectangular form, so that, in case of emergency, you know how to find rectangular form of complex number by hand.

The rectangular form is the most common way of writing down complex numbers as z = a + bi. It corresponds to representing z as a point (a, b) on a 2D complex plane. It means that z is a number with a units along the real (horizontal) axis and b units along the imaginary (vertical) axis.

The two coordinates have their names:

• a is the real part of z; and
• b is the imaginary part of z.

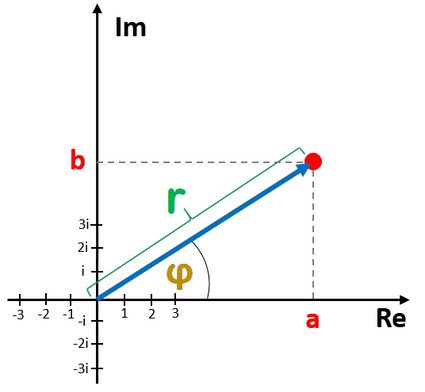
In the next section we will explain how to convert a complex number from polar to rectangular form.

If we have to convert a complex number z = r × exp(iφ) from its polar (exponential) form to rectangular form, we must recall the basic trigonometric formulas:

cos(φ) = a / r

and

sin(φ) = b / r.

Solving for a and b, respectively, we obtain

a = r × cos(φ)

and

b = r × sin(φ)

These are the formulae that we use to convert from polar form to rectangular form. They are implemented in Omni's complex number to rectangular form calculator as well.

This tool is very straightforward to use. If you want to convert polar complex number to rectangular form, input the two ingredients of the polar form: the magnitude and phase into the two upper fields of the calculator. It will immediately display the two coefficients of the rectangular form of your number: the real part a and the imaginary part b. You write them down in the a + bi form.

That's it! Never again will you have to wonder how to find rectangular form of complex number :)

Once you're done with converting polar complex numbers to rectangular form, learn how to convert to other forms as well! Omni has a rich collection of calculators that will help you master various operations on complex numbers:

• Complex number calculator;
• Complex number to polar form calculator;
• Complex number to trigonometric form calculator;
• Multiply complex numbers calculator;
• Divide complex numbers calculator;
• Imaginary number calculator;
• a+bi form calculator;
• i calculator; and
• Polar form calculator.

To convert a polar number z = r × exp(iφ) to rectangular form:

1. Compute cos(φ).
2. Multiply by r. This is the real part of your number: a = r × cos(φ).
3. Compute sin(φ) .
4. Multiply by r.
5. This is the imaginary part of your number b = r × sin(φ).
6. Your number in rectangular form reads z = a + bi with a, b computed as above.

The answer is 1/2 + (√3/2)i. To arrive at this result, we compute cos(π/3) = 1/2 and sin(π/3) = √3/2. The magnitude of exp(iπ/3) is 1. So:

• The real part is a = 1 × cos(π/3) = 1 × 1/2 = 1/2.
• The imaginary part is b = 1 × cos(π/3) = 1 × √3/2 = √3/2.