Complex Number to Trigonometric Form Calculator
Table of contents
What is the trigonometric form of a complex number?How do I find the trigonometric form of a complex number?How to use this complex number to trigonometric form calculatorOmni calculators and complex numbersFAQsThis complex number to trigonometric form calculator will help if you're still not quite sure how to find the trigonometric form of a complex number a + bi. In the brief article below, we explain what the trig form of a complex number is and how to quickly convert from rectangular to trigonometric form.
What is the trigonometric form of a complex number?
The trigonometric form of a complex number z reads
z = r × [cos(φ) + i × sin(φ)],
where:
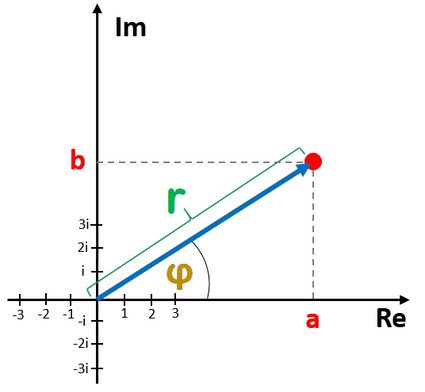
ris the modulus, i.e., the distance from(0,0)toz; andφis the argument, i.e., the angle between the x-axis and the radius between(0,0)andz.
You can see r and φ in the picture below. Using basic trigonometry, we see that
cos(φ) = a × r and sin(φ) = b × r, exactly as claimed by the formula above.
How do I find the trigonometric form of a complex number?
To convert a complex number z = a + bi from rectangular to trigonometric form, you need to determine both the magnitude and the argument of z:
- Compute the magnitude as
r = √(a² + b²). - Compute the phase as
φ = atan(b / a). If needed, correct by±πto end up in the correct quadrant of the plane. - Write down the trigonometric form as
z = r × [cos(φ) + i × sin(φ)].
How to use this complex number to trigonometric form calculator
To use the power of our tool, you need to feed it with the real and imaginary parts of your complex number, so with a and b from the a + bi form.
Our complex number to trigonometric form calculator will immediately compute the magnitude r and phase (argument) φ of your number and then display the trigonometric form in two ways: using radians and degrees.
🙋 For some particular complex numbers you will get a third form as well: it will use π × rad as the angle unit. In this way, angles like π/4 have a chance of appearing.
Omni calculators and complex numbers
Satisfied with the complex number to trigonometric form calculator? Omni Calculator features a rich collection of calculators dedicated to complex numbers! Here's a full list in case you want to learn more:
What is the trigonometric form of i+1?
The answer is i = √2 × [cos(π/4) + i × sin(π/4)]. To arrive at this result, observe that the magnitude of i equals r = √(1² + 1²) = √2. Then observe that the argument of i equals π/4 since atan(1/1) = π/4.
How do I get the trigonometric form from polar form?
If you have a complex number in the polar form r × exp(iφ), it suffices to take r and φ from the polar form and write down r × [cos(φ) + i × sin(φ)] to get the trig form of your complex number. No calculations required!