Arcus Tangent Calculator

Omni's arcus tangent calculator will help you quickly invert the tangent function. Scroll down to learn what the arcus tangent function does and what are its domain and range. The graph of the arcus tangent is, of course, included as well!

Arcus tangent is one of inverse functions in trigonometry: the inverse of tangent. In other words, it answers the question: what angle what used to produce this specific tangent value?. More formally, if the tangent of some angle α ∈ (-π/2, π/2) is equal to x, i.e.,

x = tan α

then arcus tangent allows you to recover α given x:

α = arctan(x).

Here's the graph of the arcus tangent function:

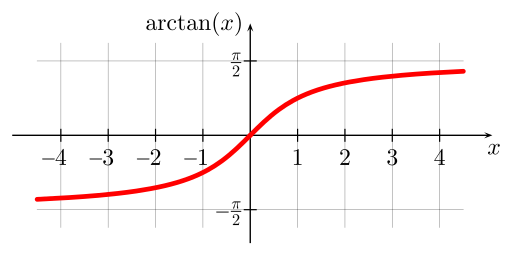
As you can see, it assumes values in the interval (-π/2, π/2). This is because tangent is many-to-one function, while only one-to-one functions have an inverse. Hence, before inverting, tangent must be restricted to an interval where it is one-to-one. This interval is usually taken to be (-π/2, π/2).

That's why we've stressed the angle α considered above is taken from the interval (-π/2, π/2).

Having discussed the range, let us say a few words about the domain of the arcus tangent function.

The domain of the arcus tangent is all real numbers. To see this, recall that the domain of an inverse function is the range of the original function. Since the range of the tangent is all real numbers, we easily get the answer.

To use this arcus tangent calculator, you just need to input the number for which you want to compute the arcus tangent. Since the domain of the arcus tangent is the whole set of real numbers, every input will do.

Tip: this arcus tangent calculator can work in reverse too! In other words, it can function as a regular tangent calculator. Just input the angle into the field y and enjoy the result!

Omni features a mini-collection of tools related to inverting the tangent function:

• Arctan calculator;
• Tan-1 calculator;
• Tan inverse calculator; and
• Inverse tangent calculator.

To determine the arcus tangent of 0:

1. Recall that arcus tangent is the inverse of the tangent function.
2. Sketch a graph of the tangent function and look for places where it crosses the horizontal axis.
3. Among the points determined in the previous step, you need to determine those that belong to the interval (-π/2, π/2).
4. The only such a point is x = 0. This is the answer you've been looking for: the arcus tangent of zero is zero.