Last updated: Jul 25, 2024

Inverse Tangent Calculator

Q: What is the value of the inverse tangent of 1?

To find the inverse tangent of 1 : Ask yourself the question, "which angle results in a tangent with value 1 ?" Picture the trigonometric circle with radius 1 . The triangle we can build with catheti of length 1 is a 45-45-90 right triangle. The angle 45° has tangent 1 : tan(45°) = 1 . The inverse tangent takes 1 as the argument and returns 45° , or π/4 as the result.

Q: How do I find the inverse tangent of 0?

The inverse tangent of 0 is 0 , which means that the function passes through the origin. We find this result by simply looking at the graph of both the tangent and its inverse. The tangent of 0 has the value 0 . Since the inverse tangent is a reflection without translations of the tangent, the crossing in the origin remains the same, and we can confirm that tan-1(0) = 0 .

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Anna Szczepanek, PhD

Anna Szczepanek

PhD, Jagiellonian University in Kraków, Poland

Website

Holds a Ph.D. degree in mathematics obtained at Jagiellonian University. An active researcher in the field of quantum information and a lecturer with 8+ years of teaching experience. Passionate about everything connected with maths in particular and science in general. Fond of coding, she has a keen eye for detail and perfectionistic leanings. A bookworm, an avid language learner, and a sluggish hiker. She is hopelessly addicted to coffee & chocolate – the darker and bitterer, the better. See full profile

Check our editorial policy

New

Table of contents

The inverse tangent function How to use our inverse tangent calculator Other inverse tangent calculator FAQs

Calculating the inverse tangent function can be a rather tricky task: discover how to do it and the characteristic of this function with this simple tool. Keep reading to learn:

What is the inverse tangent, and how we define it.
How to calculate the inverse tangent;
The graph and properties of the inverse tangent;

and much more!

The inverse tangent function

The inverse tangent function is, as the name says, the inverse function of the trigonometric function tangent. An inverse function is, by definition, a function that takes as input the result of a function and returns the argument of the original function:

y = f(x) \ \rightarrow \ x = f^{-1}(y)

Inverting a function is not an easy task, and more often than not, there are no common rules to do so.

In the case of trigonometric functions, and in particular of the tangent function, the inverse functions take as argument a dimensionless number, and return an angle. If:

y = \tan(x)

Then we define the inverse tangent function as:

x = \tan^{-1}(y)

The tangent is a periodic function, which repeats in the range $(-\pi/2,\pi/2)$ with values between $-\infty$ and $\infty$ . In the image below, you can see its graph:

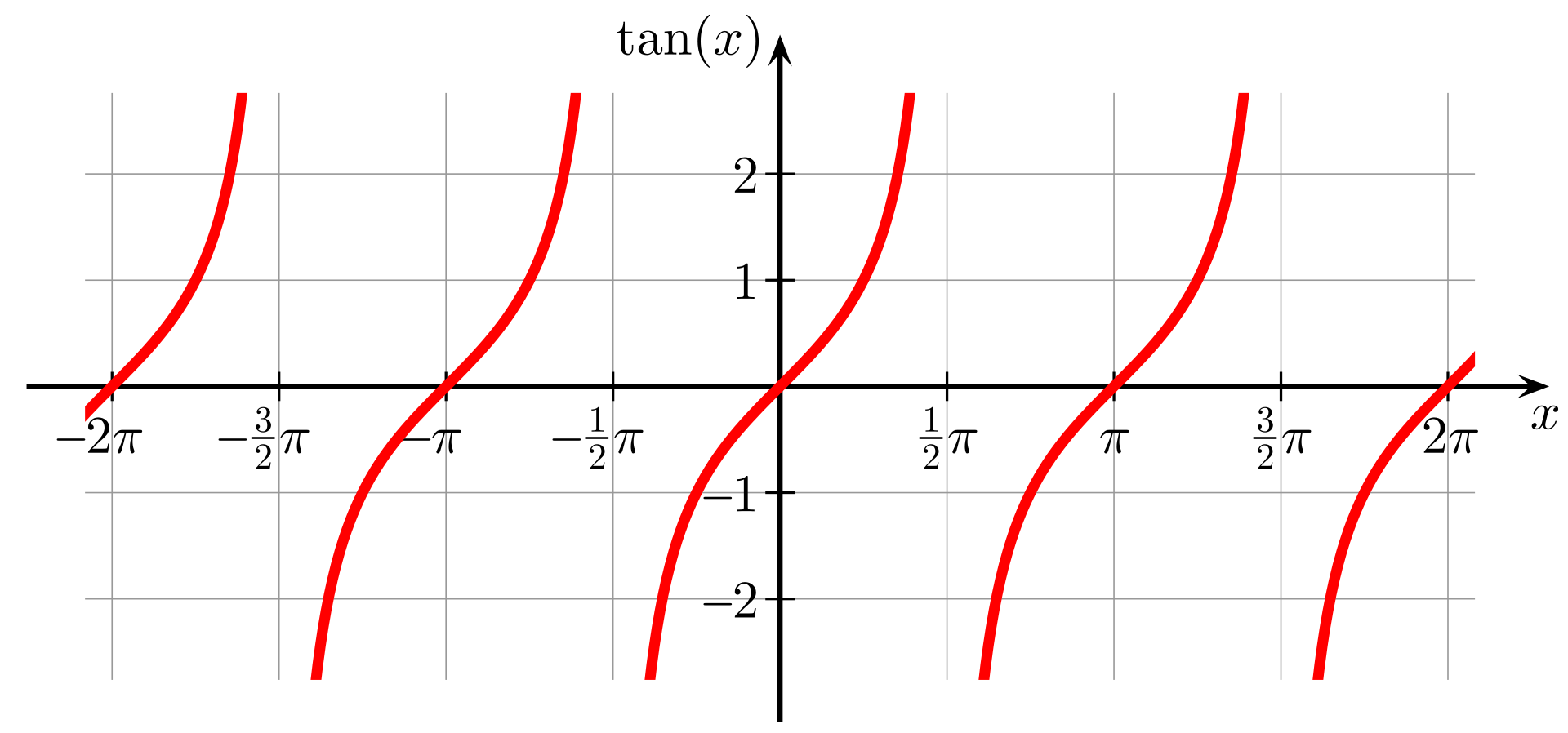
We can invert a function by taking the reflection with respect to the diagonal of the first quadrant. However, due to the periodicity of the function, we would find something that is not exactly a function since for each $x$ value we would find infinite $y$ values. To properly define the inverse tangent function, we need to restrict the domain of the tangent function to the range $(-\pi/2,\pi/2)$ . By doing so, we find a single chunk of the function, and we can define the inverse. Here is its graph:

You can clearly see that:

The inverse tangent's domain is the entire $x$ -axis.
The inverse tangent's range is restricted to $(-\pi/2,\pi/2)$ .

Note also how the inverse tangent is not periodic anymore!

How to use our inverse tangent calculator

If you are reading this text, you probably asked yourself, "how to calculate the inverse tangent?". The answer is simple: use a calculator, as there is no easy way to find the values of this function using paper and pen.

Omni's inverse tangent calculator is the perfect tool for this purpose: insert a number in the valid domain of the inverse tangent (that is, the whole x-axis), and you'll get the result in no time. You can also use our inverse tangent calculator in reverse!

Other inverse tangent calculator

The inverse tangent function is known by many different names: we created a different tool for each of them! Try our:

FAQs

Where can I find the inverse tangent?

The inverse tangent, even if originally defined in the field of trigonometry, found an important application in machine learning, where the switching of the inverse tangent from a negative to a positive value and the asymptotic behavior made it a good choice as activation function.

What is the value of the inverse tangent of 1?

To find the inverse tangent of 1:

Ask yourself the question, "which angle results in a tangent with value 1?"
Picture the trigonometric circle with radius 1. The triangle we can build with catheti of length 1 is a 45-45-90 right triangle.
The angle 45° has tangent 1: tan(45°) = 1.
The inverse tangent takes 1 as the argument and returns 45°, or π/4 as the result.

How do I find the inverse tangent of 0?

The inverse tangent of 0 is 0, which means that the function passes through the origin. We find this result by simply looking at the graph of both the tangent and its inverse.
The tangent of 0 has the value 0. Since the inverse tangent is a reflection without translations of the tangent, the crossing in the origin remains the same, and we can confirm that tan-1(0) = 0.

Related calculators

Trig Identities Calculator