Trig Triangle Calculator
If you're dealing with trigonometry and right triangles, this trig calculator for right triangles is here for you. This tool uses trigonometry to calculate these triangles, as long as you know:
- Two of its sides;
- One angle and one side; or
- The area and one side.
To learn more, keep reading this article that briefly discusses the trigonometry behind right triangles.
Right triangle trigonometry
This trig triangle calculator uses the following widely-known trigonometric ratios, which relate the sides of a right triangle to its angles:
🙋 To know how to calculate or evaluate the sine, cosine, and tangent functions, visit our trig calculator.
Additionally, we can use the inverse trigonometric functions to solve for the angles if we know the length of the sides:
🙋 To know how to calculate or evaluate these inverse functions, visit our inverse sine, inverse cosine, and inverse tangent calculators.
Let's use the following triangle to explain how this calculator solves for the different sides and angles according to the information known.
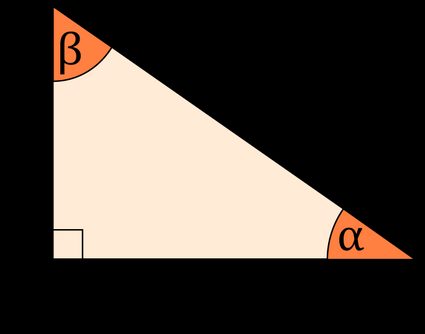
Using two sides for right triangle trigonometry calculation
Finding the third side
If you know two sides, the easiest way to find the third side is by using the Pythagorean theorem (what is the Pythagorean theorem).
- Given a and b: ;
- Given a and c: ; and
- Given b and c: .
Finding the angles
Then, we can find or by taking any of the inverse trigonometric functions mentioned previously:
Using one angle and one side for right triangle trigonometry calculation
Finding the angle
The sum of the internal angles of a triangle will always be . In a right triangle, there's a right angle () and, therefore, the sum of the other two angles ( and ) will be . Therefore:
- Given : ; or
- Given :
Finding the two missing sides
To find the two unknown sides, you can use the angle and the trigonometric ratios:
-
Given a: and ;
-
Given b: and ; and
-
Given c: and ;
Using area and one side for right triangle trig calculation
If you know or , use the right triangle area formula that relates the base () to the height () and solve for the unknown side:
- Given a: ; and
- Given b: .
Once you know at least two sides, use the second section method to obtain the angles.
Other trigonometry and triangle calculators
FAQs
What's the leg measurement of a 45-45-90 triangle of 18 cm hypotenuse?
If the hypotenuse of a 45-45-90 triangle measures 18 cm, the length of any of its two legs is 9√2 cm or 12.728 cm. To get to this answer:
-
Take the sin of any of the 45° angles, which equals any of the legs (a) divided by the hypotenuse (c):
sin(45°) = a/c
-
Solve for the leg (a):
a = c × sin(45°) -
Remember that sin(45°) = 1/√2 and input the hypotenuse c = 18 cm:
a = 18 cm × (1/√2):
= 9/√2 cm = 12.728 cm
What's the leg measurement of a 45-45-90 triangle of 10√5 inches hypotenuse?
If the hypotenuse of a 45-45-90 triangle measures 10√5 inches, the length of any of its two legs is 5√10 inches or 15.81 inches. To get to this answer:
-
You can use the formula that relates the hypotenuse (c) to any of the legs (a) of a 45-45-90 triangle:
c = a × √2 -
And solve for the leg a:
a = c/√2 = (10√5 in)/√2 = 5√10 in = 15.81 in.
