Trig Calculator

Welcome to this trigonometric calculator, a trig tool created to:

1. Calculate any trigonometric function by inputting the angle at which you want to evaluate it; and
2. Solve for the sides or angles of right triangles by using trigonometry.

Keep reading this article to learn more about trigonometric functions and the trig identities that relate them.

Trig functions are functions that take an angle as the argument. We define these functions by using the angle of a right triangle that is inserted in a unitary circle. Then, we relate that angle to the sides of such a triangle.

As the right triangle is circumscribed in a unit circle, the length of its hypotenuse equals the circle's radius (which equals one unit).

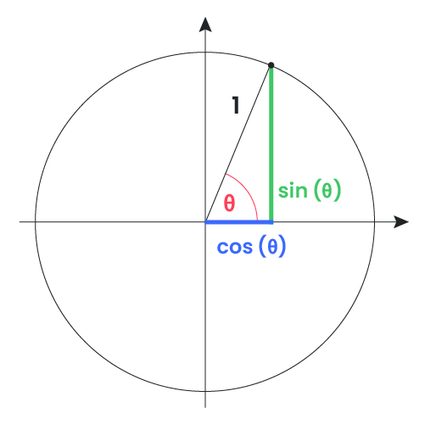
Sine and cosine are the fundamental trigonometric functions arising from the previous diagram:

• The sine of theta (sin θ) is the hypotenuse's vertical projection (green line); and
• The cosine of theta (cos θ) is the hypotenuse's horizontal projection (blue line).

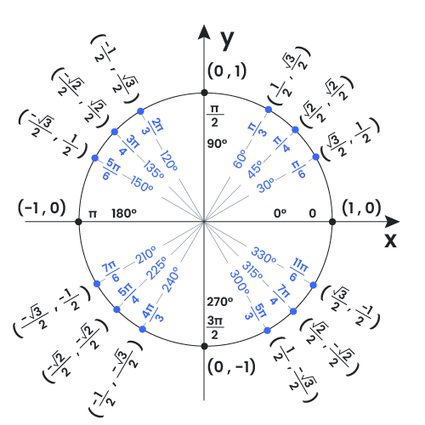
We can rotate the radial line through the four quadrants and obtain the values of the trig functions from 0 to 360 degrees, as in the diagram below:

• For example, for an angle that leads to the second quadrant (90-180°), the cosine will be negative as the horizontal projection of the hypotenuse will point to the left. That's the case of 135°, whose cosine (horizontal projection, or x coordinate) equals -√2/2.
• For the third quadrant (180-270°), the cosine and the sine of the angles lying on it will be negative.
• For the fourth quadrant angles (270-360)°, the cosines will be positive and the sines negative.

Beyond 360 degrees

The previous behavior repeats cyclically, so trigonometric functions are not limited to 360°. We can keep rotating counterclockwise, and once we reach 360 degrees, the sine and cosine functions start to repeat the same behavior. As a consequence, we can relate the functions at different angles with the following trig identities for any n integer:

• sin(θ + 2πn) = sin(θ);
• cos(θ + 2πn) = cos(θ); and

For example a trig function at 90° (π/2) will be mathematically the same as at 450° (5π/2), as 5π/2 = π/2 + 2π.

Negative angles

Negative angles imply the same way to calculate sine and cosine (vertical and horizontal projections, respectively), with the difference that angular rotation occurs in the clockwise direction. For example, a trigonometric function at 270° is the same as at -90°, as their radial lines are the same (you can check it with this calculator)

Once you know the value of sine and cosine, you can use the following trigonometric identities to obtain the values of the other four functions:

1. Tangent is the sine-to-cosine ratio

   tan(α) = sin(α)/cos(α)

2. Cosecant is the reciprocal of the sine

   csc(α) = 1/sin(α)

3. Secant is the reciprocal of the cosine

   sec(α) = 1/cos(α)

4. Cotangent is the reciprocal of the tangent

   cot(α) = 1/tan(α)

From the previous analysis, we can obtain some valuable formulas that relate the angle of a right triangle to its sides. Of course, this doesn't limit to unit circles, so we can use it for hypotenuses of any length.

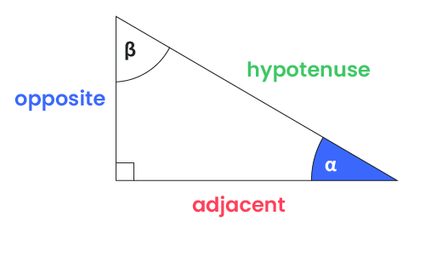
We relate the angle of the right triangle to its sides in the following way:

sin(α) = opposite/hypotenuse

cos(α) = adjacent/hypotenuse

tan(α) = opposite/adjacent

Remember that cotangent, secant, and cosecant are the inverse of the previous functions:

csc(α) = 1/sin(α) = hypotenuse/opposite

sec(α) = 1/cos(α) = hypotenuse/adjacent

cot(α) = 1/tan(α) = adjacent/opposite

You also can apply the previous formulas for the other acute angle (β), but consider that the legs of the triangle will switch: the adjacent will now be the hypotenuse and vice versa.

If you like this calculator, you may find these other tools interesting:

• Trigonometry calculator;
• Cosine triangle calculator;
• Sine triangle calculator;
• Trig triangle calculator;
• Right triangle trigonometry calculator;
• Sine cosine tangent calculator;
• Tangent ratio calculator; and
• Tangent angle calculator.