Sine Cosine Tangent Calculator

With our sine cosine tangent calculator, you will learn everything you need about the most important trigonometric functions: discover how to identify them, their relationship to right triangles, and how to calculate them in the blink of an eye!

The trigonometric functions are mathematical functions that associate numerical values to angles according to specific rules. There are many trigonometric functions, but the most important are sine, cosine, and tangent. Since they take an angle as an argument, it's natural to identify them on a circle.

In the image below, you can see a trigonometric circle, a circle with radius $1$ where for a specific angle $\alpha$, we highlighted the segments corresponding to sine and cosine.

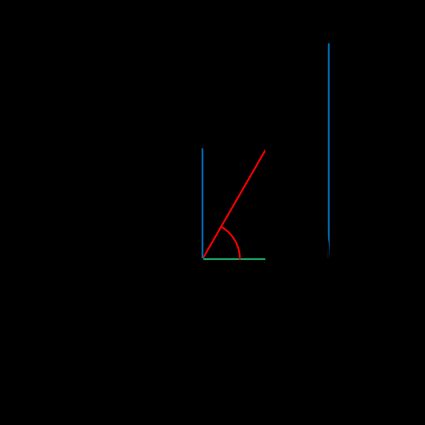
Note how the tangent lies outside of the circle, tangent to it, as the name says. While sine and cosine are readily identifiable as the projections of the radius on the vertical and horizontal axis, we need to see the definition of the tangent to understand how to find it and visualize it:

In the picture below, we represented the three trigonometric functions: we calculated sine, cosine, and tangent values for the angles between $0\degree$ and $360\degree$.

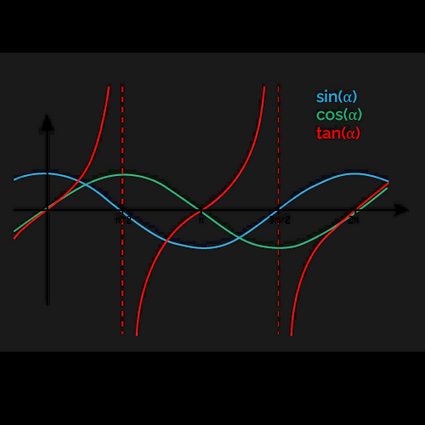
Even from this quick peek into trigonometry, you can identify many properties of these functions:

• The values calculated for sine, cosine, and tangent are periodic. In particular:
  • Sine and cosine have periodicity equal to $360\degree$; and
  • The tanget has periodicity $180\degree$.
• Sine and cosine have values comprised between $-1$ and $1$. The tangent assumes values between $-\infty$ and $\infty$.
• Sine and cosine switch values periodically in the four quadrants of the circle;
• Sine and cosine are "out of phase" by $90\degree$ with each other.

Keep exploring these functions to discover many other, almost endless, properties!

After this introduction to trigonometric functions, it's time to learn how to calculate sine, cosine, and tangent in a triangle. Jump to the next section!

Right triangles and trigonometric functions share a deep connection: you can calculate the values of the latter and the geometric characteristic of the former swiftly without remembering any formulas: thanks to the neat graphic representation of the functions, you can always draw what you need on a piece of paper, and you'll recall the math in no time!

To understand the connection between right triangles and trigonometric functions, look at the detail of the previous image.

We took an angle and highlighted the values of sine and cosine. As you can see, sine and cosine form a right angle; thus, they correspond to the catheti (legs) of the triangle. The radius of the circle becomes the hypotenuse. Immediately, you can identify the fundamental relationship between sine and cosine:

which we obtain from the Pythagorean theorem. But this alone would not tell us how to calculate sine, cosine, and tangent in a triangle. If you consider the angle $\alpha$, you can find the values of the functions thanks to a set of ratios between the lengths of the triangle's sides:

By rotating the triangle and placing the desired acute angle in the center of the trigonometric circle, you can calculate sine, cosine, and tangent for the second angle, too.

Our sine, cosine, and tangent calculator allows you to see the values of the trigonometric functions directly for a specific angle. You can also insert the known information about a right triangle and see if they are enough to calculate the rest. If you found this tool useful, check out our other calculators:

• Trigonometry calculator;
• Cosine triangle calculator;
• Sine triangle calculator;
• Trig triangle calculator;
• Right triangle trigonometry calculator;
• Trig calculator;
• Tangent ratio calculator; and
• Tangent angle calculator.