Inverse Cosine Calculator

The inverse cosine calculator will quickly solve your doubts about this useful function. Keep reading this short article to learn:

• What is the inverse cosine;
• The domain and range of the inverse cosine;
• How to calculate the inverse cosine;

And much more!

The inverse cosine is the inverse function of the cosine. Let's analyze these two concepts separately:

• An inverse function is a function that reverses the action of another function. If we consider the function $y = f(x)$, we define the inverse function as $x = f^{-1}(y)$. As you can see, the inverse function takes as an argument the output of the original function and returns the original input. Inverting the function correspond, in graphical terms, to reflect the function with respect to the diagonal of the first quadrant.
• The cosine is a basic trigonometric function that corresponds to the horizontal projection of the radius of a circle at a certain angle $\alpha$.

Let's take a look at the cosine function.

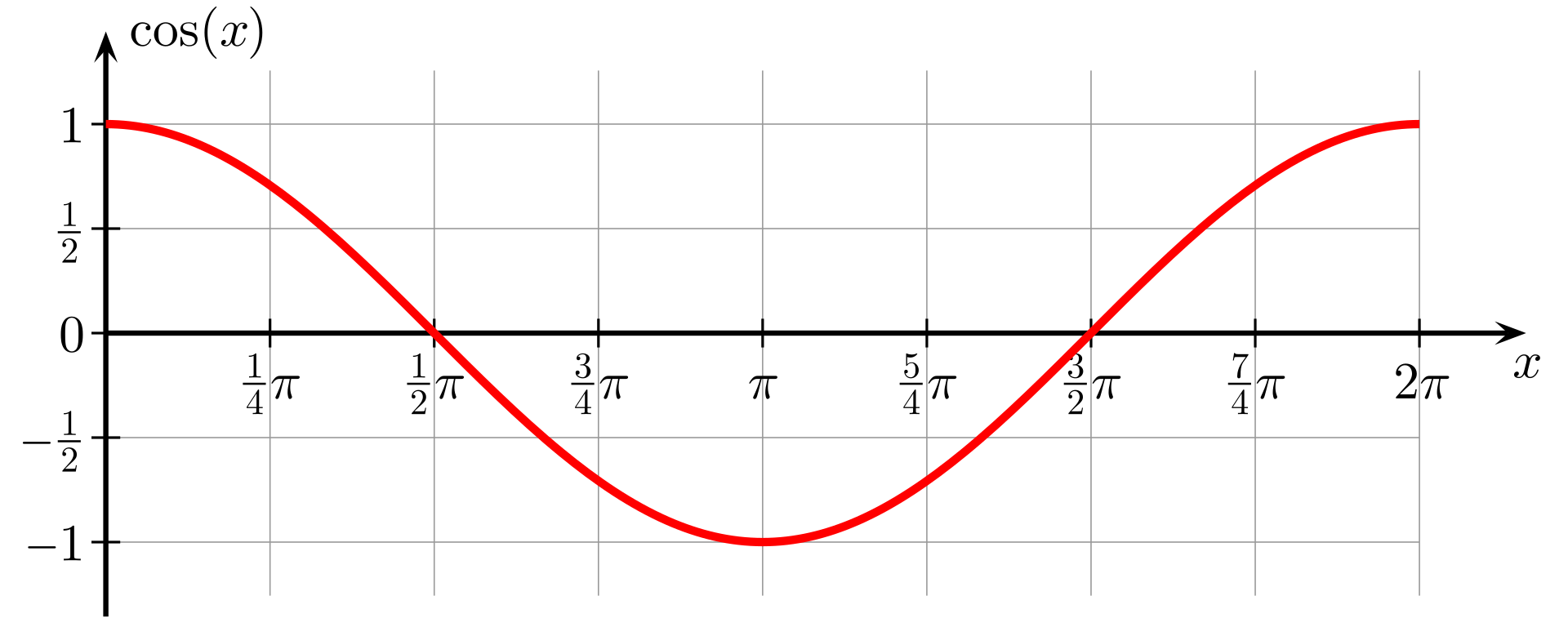
The cosine is a periodic function, which means the values it assumes between $0\degree$ and $360\degree$ repeat cyclically. The periodicity of the function means that the cosine's domain is the entire x-axis. The values of the function are entirely comprised in the range $[-1,1]$.

These two pieces of information allow us to define the domain and range for the inverse cosine function:

• The domain is $[-1,1]$; and
• The range is $[0\degree,360\degree]$.

In the picture below, you can see the inverse cosine graph:

The inverse cosine takes as its argument a dimensionless number and gives an angle as a result: these quantities are what you are going to find on the horizontal and vertical axis when defining the inverse cosine function.

Calculating the inverse cosine function is no easy task: apart from a small set of neat values, using a calculator to find its value from any real number in the domain is often the only way to work your way through this function: that's where Omni's inverse cosine calculator comes in handy!

Anyway, here are the most important values of the inverse cosine:

• $\arccos(0) = 90\degree$;
• $\arccos(1/2) = 60\degree$;
• $\arccos(1/\sqrt{2}) = 45\degree$;
• $\arccos(\sqrt{3}/2) = 30\degree$; and
• $\arccos(1) = 0\degree$;

Maybe you want to introduce your students to the inverse cosine function under another name: we made these calculators for you:

• The arccos calculator;
• The cos inverse calculator; and
• The cos-1 calculator.

The domain of the inverse cosine is [-1,1]. This interval corresponds to the range assumed by the cosine function, which has a minimum at 180° and a maximum at 0°.

The inverse cosine of 1/√2 is 45°. To find this result, follow this reasoning:

1. What is the angle that has cosine equal to 1/√2? The answer is 45°.
2. Call the angle x, and the result y: y = cos(x). Remember that by definition, the inverse cosine is the function x = arccos (y).
3. We then substitute the values found before:
   cos(45°) = 1/√2
   And:
   arccos(1/√2) = 45°.

To find the inverse cosine of 0, use a graphical approach:

1. Remember that the inverse cosine is nothing but the reflected cosine function.
2. Trace the graph of the cosine function between 0° and 180°, and find the point where the function crosses the x-axis: you will find cos(90°) = 0.
3. You found the result of the inverse cosine of 90°: simply write arccos(0) = 90°!