Torus Surface Area Calculator

This torus surface area calculator will assist you to estimate the surface area of a torus for a given pair of radii. You must have encountered this shape in daily life on your plate as a doughnut or a bagel, or on the roads underneath vehicles 😉. The life-saving tube or ring, aka the rescue buoy, is also a torus. The torus likewise has significance in mathematics and physics. Read on to understand what is a torus and how to calculate the surface area of a torus.

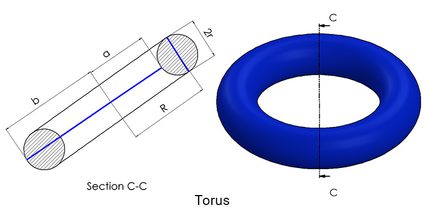
A torus is a 3D shape obtained by revolving a circle around an axis. This shape is commonly found in doughnuts, rings, tires, tubes. If you take a ring and circularly trace around a pencil, you get a torus. In modern design software, it is fairly easy to draw them by using a revolve command with a circle as a cross-section. A torus has two radii – the first radius is the radius of the cross-section r, and the second radius R is the radius of revolution, which is the distance between the center axis and the center of cross-section.

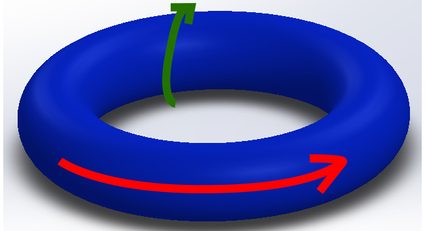
Any point on a torus is defined using a modified coordinate system having two directions – toroidal (red arrow) and poloidal (green arrow).

Based on the combinations of the two radii, we can obtain multiple types of tori. Such that:

• Ring type (R > r)
• Horn type (R = r)
• Spindle type (R < r)

In addition to these radii, the torus can also be expressed in the form of two radii, such as inner (a) and outer radii (b) of the torus. Mathematically, that's:

a = R - r
b = R + r

The surface area A of the said torus is:
A = 4 * π² * r * R
The surface area can also be written in terms of inner and outer radii:
A = π² * ( b - a ) * (b + a)
The above equation is used in the calculator to determine the surface area where:
r = (b - a) / 2
R = (a + b) / 2

Note: This calculator only applies to ring type or horn type tori. Furthermore, in the case of a horn-type torus, i.e., R = r, minor radius, a becomes zero.

Follow three simple steps to find out the surface area of a torus.

• Step 1: Enter the inner radius of torus, a.
• Step 2: Enter the outer radius of torus, b.
• Step 3: The calculator will now use the above formula to return the surface area of a torus.

Find the surface area of a horn-type torus having a radius of cross-section r = 1 m.
Note: The torus is of horn type, i.e., r = R.

Let us first convert the radii into the inner and outer radius, a and b.

a = R - r = 0 m
b = R + r = 1 m

• Step 1: Enter the inner radius of torus, a = 0 m.
• Step 2: Enter the outer radius of torus, b = 1 m.
• Step 3: The torus surface area calculator will now return:

V = π² * ( b - a ) * (b + a)
V = π² * (1 - 0) * (1 + 0) = 9.87 m²
The surface area for the torus is 9.87 m². You might also be interested in determining the volume of a torus.