Circle Calculator

This area of a circle calculator will help you determine the circumference, diameter, area, and radius of any circle.

In the article below, you will find all the circle formulas you will ever need to calculate one of these values. Read on if you're looking for the circle definition or want to understand how to find the center of a circle or circumference of a circle – or what pi is.

Also, you'll find information below about the unit circle and the properties of a circle, not to mention some fun facts about this shape - if you want to know what's the roundest country in the world, keep scrolling!

We use the following notation:

• c stands for circumference,
• d for diameter,
• a for area, and
• r for the radius of the circle.

Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you:

A circle is a planar closed curve made of a set of all the points that are at a given distance from a given point - the center. Alternately, you can define the circle as the locus of points at the same distance from a given fixed point. The name circle derives from Greek, meaning hoop or a ring.

The circle, technically speaking, is only the boundary, not the area inside the shape. The whole figure is called a disc. A disc may be closed if it contains the circle that constitutes its boundary and open if it doesn't. In everyday use, the circle is sometimes understood as the disc – the plane surface bounded by such a curve.

Circle terminology consists of the definitions of:

• Circumference – the distance around the circle;
• Radius – a line segment joining the center of the circle with any point on the circle;
• Diameter – a line segment whose endpoints lie on the circle and which passes through the center; and
• Chord – a line segment whose endpoints lie on the circle.

There are many other terms associated with the circle – such as the arc, secant, or tangent – but for our basic explanations, you need to understand only the ones described above.

A circle is a simple, distinctive shape with many unusual properties:

• Has the largest area for a given length of perimeter;
• Highly symmetric – reflection symmetry occurs for every line through the center, rotational symmetry around the center for every angle; and
• May be constructed through any three points on the plane (not all on the same line). Such a circle is a unique circle.

Moreover, all circles are similar, and unique circles in every triangle may be inscribed and circumscribed. A circle has dozens of other interesting properties, which you can discover on your own.

The most popular equations associated with the circle are:

1. Circle area

   a = πr²

2. Circle circumference

   c = 2πr

3. Circle diameter

   d = 2r

You can derive many other circle formulas from the above equations, which you'll find in the dedicated paragraphs below.

If you're looking for the circle formula itself, check out this equation of a circle calculator.

The unit circle is a circle with a radius of one. Usually, its center is positioned at the origin (0, 0) in the Cartesian coordinate system.

Let's choose any point (x, y) on the unit circle. Then |x| and |y| are the lengths of the right triangle legs, with the radius of our circle being the hypotenuse of length 1. Using the Pythagorean theorem, we can find out that:

x² + y² = 1

As x² = (−x)², the above equation works for every quadrant, not only the first one.

Also, we can define the right triangle legs in terms of sine and cosine:

cos(α) = x / 1 = x

sin(α) = y / 1 = y

Then:

sin²(α) + cos²(α) = 1

This equation is known as the Pythagorean trigonometric identity. To transform stresses, you can apply this on mohr's circle.

c is the circle's circumference – that is, the total length of the line you draw with a compass. You can calculate it in the following ways:

1. If you know the radius or diameter of the circle:

   c = 2πr = πd

2. If and radius and diameter are unknown, then:

   c = 2√(πa)

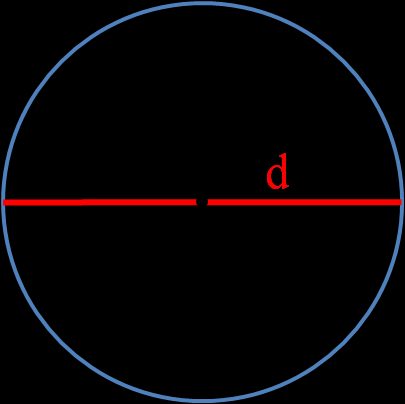
d is the diameter of a circle – the length of a line that passes through the center point and joins two points on the circle. You can determine it with these equations:

1. If you know the radius of the circle:

   d = 2r

2. If radius and area are unknown:

   d = c / π

3. If radius and circumference are unknown:

   d = 2√(a / π)

a stands for the area of the circle. It is the only value expressed in squared units (for example, cm²). You can calculate it as follows:

1. If you know the radius or diameter of the circle, the area of the circle formula is:

   a = πr² = π × (d / 2)²

2. If radius and diameter are unknown, you can calculate it from the circumference:

   a = c² / 4π

If you are interested in calculations of some fraction of a circle, check:

• Our dedicated semicircle area calculator to find the area of half a circle;
• Sector area tool to check the area of a pizza slice; or
• Segment area calculator – useful if we want to determine the area of the cross-section of partially filled pipe.

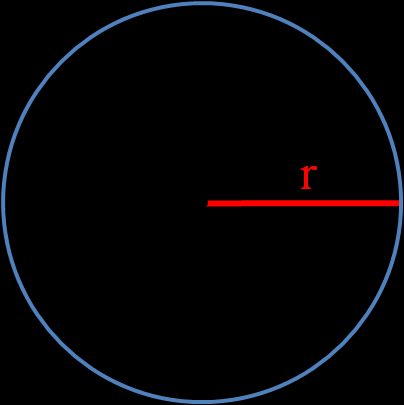
r, or the circle's radius, is the length of a line that joins the center point with any point lying on the circle. You can find it with the following formulas:

1. If you know the diameter of the circle:

   r = d / 2

2. If diameter and area are unknown:

   r = c / 2π

3. If diameter and circumference are unknown:

   r = √(a / π)

There are many ways to find the center of a circle. Here we'll show you two constructional methods:

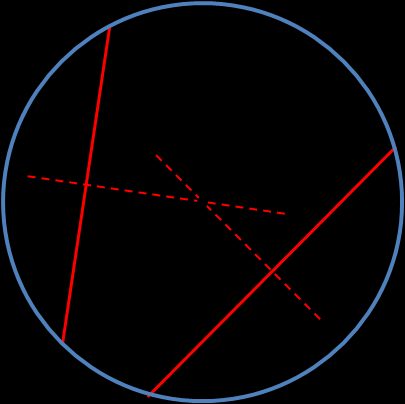
Method 1 is a simple technique to find the center of a circle using a compass and a straightedge:

1. Using a straightedge or a ruler, draw any two chords.

2. Construct the perpendicular bisectors of one of the chords. Use a compass to draw two overlapping circles (their centers at the endpoints of the cords, the same radius). The circles will intersect in two points – draw a line through them using a straightedge.

3. Repeat the construction of the bisector procedure for the second chord.

4. Two bisectors will cross each other at one point; this is the center of a circle.

If you want, you can draw the third chord and its bisector to increase – and check – the accuracy of the center of a circle determination.

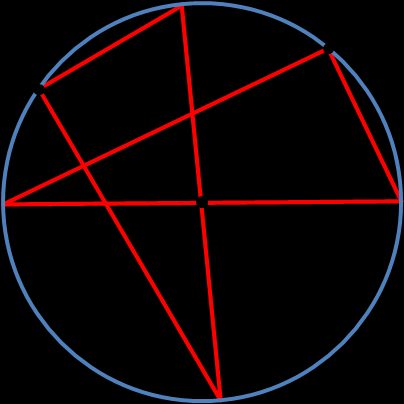
Method 2 is only a rough estimation of a center of a circle, but if you don't need great accuracy, you can use this technique:

1. Choose a point on the circle.

2. Take something which has a 90-degree angle and straight edges. It may be a triangle measuring tool, but also anything you have at hand - e.g., a book, cardboard, or a sheet of paper. Place the triangle in such a way that the right angle is touching our chosen point.

3. Draw two perpendicular lines across the circle. Mark the points where they intersect with the circle.

4. Draw a straight line through the points. This is the diameter of the circle.

5. You can find the center of a circle by:

   • Constructing the bisector of the diameter (as in the first method); or
   • Simply repeating the procedure – choosing another point on the circle, drawing perpendicular lines, and creating another diameter. The intersection of two diameters will show us the center of a circle.

A chord is a line segment joining two points on any curve – this curve may be a circle but also, e.g., an ellipsis. If a chord of a circle passes through the center of a circle, it's called the diameter and is the longest chord possible.

The chord of a circle was widely used in ancient trigonometry. Even though we substituted it with trigonometric functions, especially sine, it's still good to know how to calculate its length on a unit circle:

chord(α) = √[(1 - cos(α))² + sin²(α)] = √[2 - 2cos(α)] = 2sin(α/2),

where α is a central angle, taken in the positive sense, and must lie in the interval 0 < α ≤ π.

We can also take the chord length of any size of the circle by multiplying the unit circle chord by the circle's radius, r, as shown in this equation below:

chord(α) = r × 2sin(α/2)

Concentric circles are circles with a common center. The ring-shaped object – the region bounded by two concentric circles of different radii – is called an annulus.

What are real-life examples of concentric circles?

• The target in archery or a dartboard.
• Circular ripples on water.
• Growth rings of trees (approximately).
• Grooves on a vinyl record or CD.

Pi is the most well-known mathematical constant. It's a ratio of a circle's circumference to its diameter:

π = circumference / diameter

Regardless of the circle's size, the ratio c/d is constant. Usually, the pi constant is approximated to a couple of digits, e.g., four or six. The first 40 decimal digits are:

π ≈ 3.1415926535897932384626433832795028841971...

The π is an irrational number, meaning that no finite number of digits can represent π exactly (and they never repeat). Pi has been calculated to over twenty-two trillion digits beyond its decimal point, and this number is still rising with the development of computing technology.

There are competitions in which contestants try to memorize as many digits of pi as possible. The world record certified by Guinness World Records is 70,000 digits, whereas a retired Japanese engineer holds a non-official record of over 100,000 digits.

Did you know that...

• There's a style of writing called pilish. The lengths of consecutive words match the digits of the pi. For example:

  • May I have a large container of coffee beans – 314159265 in pilish, if nine digits to remember is enough; and

  • How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics! – for fifteen digits.

  That's an excellent method to memorize the pi digits, as the brain is far better at remembering words than vast strings of numbers. Maybe you'll exercise your mind and invent your own pilish story?

• Several books about the pi constant have been published. There are, of course, standard mathematical essays among them, but not only – even full books are written in pilish! The one called "Not A Wake: A Dream Embodying π's Digits Fully for 10000 Decimals" by Mike Keith holds the record of the longest pilish text with 10,000 digits.

• There's a Pi day celebrated by many π enthusiasts. It's on March 14, as the date suggests (3/14). A few years ago, in 2015, there was a "special" Pi day, as the next two digits appeared in the date (3/14/15). And time – 9:26:53 – added even more digits! How can you celebrate this special geek day? Dress like Albert Einstein (he has his birthday on Pi day) and eat circular treats all day: from obvious pies (πs?) to pancakes to almost-perfectly-round pizzas.

• Although learning π to hundreds or thousands of digits may be fun (?), it was determined that only 38 decimal places are enough to measure the circumference of the observable Universe, with the accuracy of the width of a hydrogen atom. Check out the video about π and the size of the Universe by mathematician James Grime on the Numberphile channel.

In everyday use, squaring the circle is a metaphor for struggling with difficult or even impossible tasks. But what does it mean from a mathematical point of view?

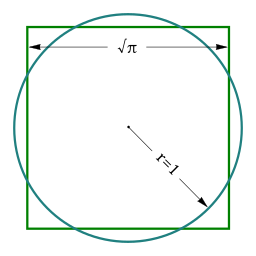
It's been a problem for mathematicians since antiquity. It's the task of constructing a square equal in area to a circle but using only a straightedge and compass. The problem was proved impossible to solve in 1882 when mathematician Lindemann showed that π is a transcendental number; thus, π and √π cannot be constructed. However, if we remove the constraint of ruler and compass, the problem is easy and was already solved and described many times.

You can meet the square and circle word combination in everyday life: boxing and wrestling rings are known as squared circles. The name comes from the traditional shape of a ring.

A circle is a 2D shape that serves as a base in some 3D curvilinear geometric shapes.

A cylinder has two parallel (usually circular) bases. Also, the one and only base of a cone is most frequently a circle.

As we know the area of a circle formula, we can easily calculate the volumes of such shapes:

v(cylinder) = πr²h

v(cone) = πr²h/3

When it comes to a sphere, it's a perfectly round geometrical object in 3D space that is the surface of a completely round ball. It's analogous to the circle and disc - but it's in three, not in two dimensions.

Also, the term a circle of a sphere exists, and it's a circle that lies on a sphere.

A great circle is the one whose plane passes through the center of the sphere; any other is called a small circle. It's used, e.g., in cartography and geography – the equator is the only great circle in the parallels of latitude family. However, all meridians of longitude, paired with their opposite meridian, form great circles.

We can compare countries in many ways – by their area, population, or GDP but have you ever wondered what's the roundest country in the world?

A mathematician and a blogger, Gonzalo Ciruelos, calculated the roundness parameter and created the ranking. The winner in the roundness category is Sierra Leone, while the title for the least round country in the world goes to the Marshall Islands.

Sierra Leone is 1st for circularity, but it's also 14th in another ranking – the world's most rectangular country! To make it even more confusing, the 4th-roundest country – Vatican City – is the world's 2nd most rectangular country, and Poland, 5th in the roundness classification, is 10th in the rectangular ranking. How is it even possible to be rectangular and round at the same time?!

It's all about the definition of rectangularity and roundness, which may not be adequate for complex or scattered shapes – and the borders of nations usually are.

You can find a better explanation and discussion of the results on the bigthink website.

If you're still unsure how to use our circle calc, let's have a look at this illustration:

1. Assume that we want to work out the size of an exemplary crop circle. We'll choose the one inspired by Euler's identity, found in 2010 at Wilton near Marlborough, UK. Euler's identity is a special case of Euler's formula (which may be derived from the unit circle in the complex plane).

2. Type the given dimension into the circle calc. We know that the crop circle was approximately 300 ft in diameter. If you need to change the units, click on the unit name and choose the one you need from a drop-down list (feet in our case).

3. Here you go! Thanks to this amazing tool, you found out all the circle parameters in the blink of an eye! Now we know that the:

   • Circumference of a circle is equal to 942.5 ft (or 314.16 yds);
   • Radius is 150 ft; and
   • Area is 70,686 ft² – or 1.6227 ac or almost the area of a soccer field! (To be more exact: ~92% of a soccer field area.)

Experiment with the calculator, and try it out yourself. On the topic of circles, why not check what's the circumference of your bike wheel?

Typically, by C, we denote the circumference of a circle, which is the distance around a circle. If you know the radius, then C is equal to 2 π × radius.

Yes, to find circumference from diameter use the formula C = π × diameter. This follows from the fact that diameter = 2 × radius, which we can substitute in the famous formula C = 2π × radius.

To determine the area of a circle from its circumference, follow these steps:

1. Square the circumference, i.e., compute c².
2. Divide the result by 4π.
3. That's it! We have just applied the formula a = c² / 4π, which links the area of a circle to its circumference.

The answer is 2√π ≈ 3.54. This is because c² = 4π × area, and so, taking the square root and plugging in area = 1, we obtain c = √(4π × 1) = 2√π ≈ 3.54.