Equation of a Circle Calculator

No matter your proficiency in the geometry of a circle, the equation of the circle may still make your head spin. If this is the case, don't worry! This standard equation of a circle calculator will help you determine a circle's radius and center coordinates in a blink of an eye. If you are curious about how to find the equation of a circle, scroll down, and you'll find an explanation of the formula.

If the geometric shape you're trying to analyze looks a bit squashed, it's probably an ellipse. In such a case, head straight to our ellipse calculator!

The standard equation of a circle is a way to describe all points lying on a circle with just one formula:

$(x, y)$ are the coordinates of any point lying on the circumference of the circle. It means that as long as you know all of the constants, you can input any $x$ value to figure out the coordinates of any arbitrary point on the circle.

$(A, B)$ are the coordinates of the center point. Just be careful about the + and - signs here; for example, a circle with an equation of the form $(x - 3)^2 + (y + 3)^2 = 5^2$ will have a center point at $(3, -3)$.

$r^2$ is the radius of the circle raised to the power of two, so to find the radius, take the square root of this value.

Our equation of the circle calculator finds not only these values but also the diameter, circumference, and area of the circle – all to save you time!

The equation of a circle may be defined in different ways; not only in the standard form shown above. A circle can also be described as the locus of all the points that satisfy the equations:

where:

• $(x, y)$ – Coordinates of any point on the circle, as before;

• $r$ – Radius of the circle; and

• $\alpha$ – Angle subtended by the point at the circle's center.

If you shift the center of the circle to (A, B) coordinates, you'll simply add them to the x and y coordinates to get the general parametric equation of a circle:

As above, you should be careful about the signs of the center point.

To demonstrate that these two forms of the circle formula are equivalent, let's do a conversion between them.

1. Starting from the parametric equation, we know that:

2. Let's take the well-known Pythagorean trigonometric identity:

3. Combine the identity with the parametric equations:

4. Then remove the parentheses:

5. And finally, multiply by $r^2$ (letting $r = 1$) and put the elements in the right order:

Here we are! That's the standard equation of a circle.

OK, you've learned about different circle equations. But where are they come from? Let's find out!

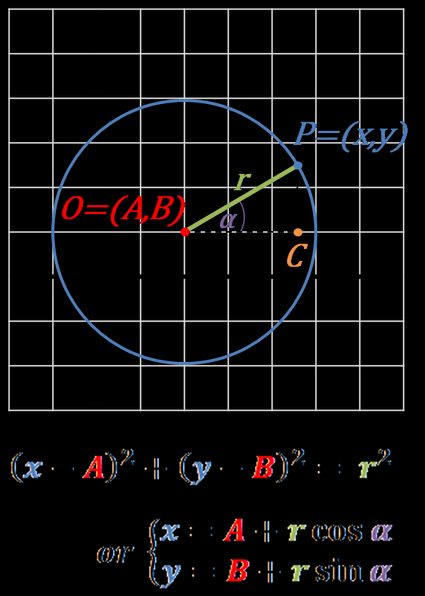
1. Choose your circle's center, $O = (A, B)$. Don't choose it as the origin of the coordinate system.
2. Draw a circle with a chosen radius $r$.
3. Pick any point on the circle. Assume the coordinates of that point are $P = (x,y)$.
4. The angle POC is equal to $\alpha$.

Great, we have all the data needed. Now we only need to use one geometric law or a basic piece of trigonometry to tie the given values together:

• Use the distance formula:

Square this obtained formula to get the standard equation of a circle:

• Use the Pythagorean theorem:

  $r$ is a hypotenuse of a right triangle POC, so from Pythagorean theorem we can write:

Also, we know that:

Coming back to the first equation, we get:

This is because $a^2 = (-a)^2$. the above equation works for every quadrant, not only the first one.

Then the equation can be simplified to a standard formula:

• Use trigonometry:
  Express the POC triangle sides using sine and cosine functions:

Coordinates of point P may be expressed as:

The two last equations represent the parametric equations of the circle.

Now, as you know how to find the equation of a circle, give this calculator a try!

Quite often, you will come across another form of the circle equation. It looks like this:

This is the general form of a circle equation – the same as the standard form but expanded. It is possible to get to the standard form from here with just a few simple operations – all you have to do is follow the steps below!

1. Start with your general equation, for example:

2. Put the x's and y's together:

3. Move the constant to the right-hand side of the equation:

4. Now, complete the square for x. To do this, you need to take half of the 4, square it, and add to both sides:

5. Repeat the previous step, this time completing the square for y:

6. Simplify the x- and y-terms according to the factoring formulas:

You're done – this is the standard form of a circle with a center at $(-2, 3)$ and a radius equal to $\sqrt5$.

Naturally, you don't have to go through this whole process by yourself. Use this equation of a circle calculator instead!

If you are still unsure how to use our tool, have a look at this simple example below.

1. Assume you want to use the standard equation of a circle. So it's the first part of the calculator.

2. Type the given data. Let's say that your equation of a circle parameters are equal to A = 7, B = -2, and C = 9.

3. Tadaa! The equation of a circle calculator did the job! The tool will show you what the parameters are in the other forms of an equation, explaining what the A and B values are (the circle center coordinates), and it will additionally calculate other values such as:

   • Radius – which is equal to 3 for our circle;
   • Diameter – 6 in our case;
   • Area is 28.3 for our example; and
   • Circumference of the circle is equal to 18.85.

In this calculator, we didn't put any units; you don't need them in many cases because you're working with the coordinates. If you need some units, e.g., inches, feet, or centimeters, just add them to the obtained results. Don't forget that the circles area will have squared units of length!