Mohr's Circle Calculator

Mohr’s circle calculator lets you calculate the principal stresses from a 2D stress state (see stress calculator for more). Utilizing the values of normal stresses and shear stresses on a body, the calculator will return to you the principal stress of the system. The stresses are regarded as one of the most fundamental aspects in designing any body or system (metal, for example). To this end, the calculator incorporates Mohr’s circle equations.

Read on to understand what principal stress is (refer principal stress calculator) and how to draw Mohr's circle. The article below contains an example of Mohr's circle. Using this calculator you can calculate — principal stresses — minimum and maximum, maximum shear stresses, angle of orientation, along with von Mises and mean stress. The maximum stress comes in handy to find stress concentration factor. You can also visit our stress concentration factor calculator for more on the topic.

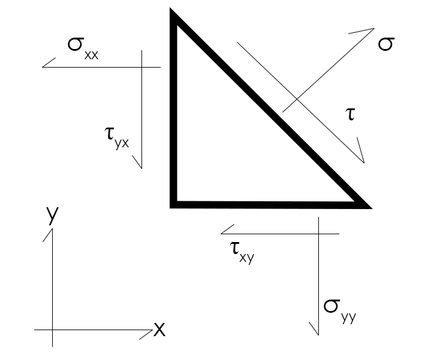
A stress state of a body is the combination of stresses at a point considering all three directions, i.e., $X$, $Y$, and $Z$ or $1$, $2$, and $3$. There are three normal stresses (acting perpendicular to the face) namely, $\sigma_{11}$, $\sigma_{22}$, and $\sigma_{33}$ and six shear stresses (acting along the plane) $\tau_{12}$, $\tau_{23}$, $\tau_{13}$, $\tau_{21}$, $\tau_{32}$, and $\tau_{31}$,. The stresses acting on the body are shown in the figure below.

Considering equilibrium acting on the body, the shear stresses can be reduced to three values, i.e., $\tau_{12} = \tau_{21}$, $\tau_{13} = \tau_{31}$, and $\tau_{23} = \tau_{32}$. Therefore, a stress state can be defined by six stresses, i.e., three normal stresses and three shear stresses. Now, if one considers only in-plane directions, the resultant stress state can be obtained by reducing the stresses, $\tau_{13} = \tau_{31} = 0$, and $\tau_{23} = \tau_{32} = 0$. The 2D stress state can now be defined using 3 stresses, i.e., two normal stresses ($\sigma_{11}$, $\sigma_{22}$) and a shear stress ($\tau_{12}$). This can alternatively be shown as given in the figure below (with 1 and 2 directions as x and y).

Consider a state at which only normal stress act on the plane. The stresses at that state are known as principal stresses. This is obtained by transforming the current stress state, i.e., reducing the shear stresses to zero.

Mathematically, the principal stresses can be written using the principal stress equation:

where $\sigma_1$ and $\sigma_2$ are minimum and maximum principal stresses. Similarly, the maximum shear stress ($\tau_\mathrm{max}$) for the state can be given by the equation:

Alternatively, maximum shear stress can also be defined using the principal stresses as:

and the mean stress ($\sigma_\mathrm{mean}$) is written as:

The angle of orientation, $\theta$ is given by:

The above set of equations helps you in drawing Mohr's circle and vice versa. The Mohr's circle equations can also be derived or obtained using the geometrical approach as given in the following section.

In order to utilize Mohr's circle to estimate principle stress, first, you need to understand what is Mohr's circle and how to draw a Mohr's circle. A Mohr's circle is a graphical representation of a stress state and is used to perform stress transformations. To draw a Mohr's circle for a given 2D stress state with normal stresses ($\sigma_{xx}$ and $\sigma_{yy}$) and shear stresses ($\tau_{xy}$ and $\tau_{yx}$):

1. Plot the coordinates ($\sigma_{yy}$, $\tau_{xy}$) and ($\sigma_{xx}$, $\tau_{xy}$) as points $A$ and $B$, respectively with $\sigma$ as X axis and $\tau$ as Y axis.
2. Join the points, $A$ and $B$ to obtain diameter $AB$.
3. Find the center of the circle, $O$, i.e., the point at which line $AB$ intersects the X-axis.
4. Draw the circle with the center point as $O$.
5. The points at which the circle intersects $X$-axis are the principal stresses.

Follow the steps below to use the principal stress formula and Mohr's circle calculator.

1. Enter the normal stress in X direction, $\sigma_{xx}$.
2. Insert the normal stress in Y direction, $\sigma_{yy}$.
3. Fill in the shear stress, $\tau_{xy}$.
4. Mohr's circle calculator will now use the principal stress equations to calculate maximum and minimum principal stresses, maximum shear stress, angle of orientation, von Mises and mean stress.