Segment Area Calculator
Use this segment area calculator to quickly compute the area of a segment. It can also be used to find chord length and arc length. If you're unsure what a segment of a circle is or even what a chord of a circle is, don't feel embarrassed – just scroll down to find a few definitions and some self-explanatory images.
What is a segment of a circle? ⌓
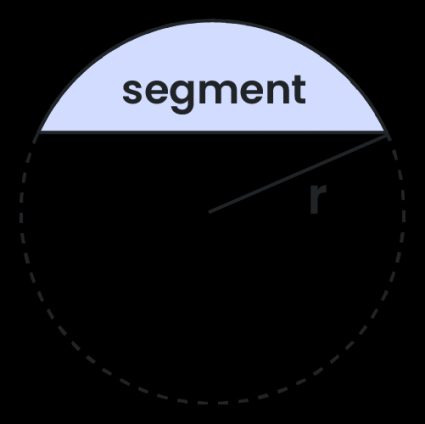
If you want to understand what the segment of a circle is, try to imagine cutting part of a circle off with a single, straight cut. And that's it! You've just created two parts of the circle, and the smaller one is called the circular segment. A more formal mathematical definition says that:
A circular segment is a region bounded by a chord and the arc of a circle (of less than 180°)
If it's equal to 180°, then it's simply a half circle – semicircle. According to some definitions, the central angle doesn't need to be smaller than 180° – in that case, you can say that cutting a circle with a line gives you two segments: a major segment and a minor segment.
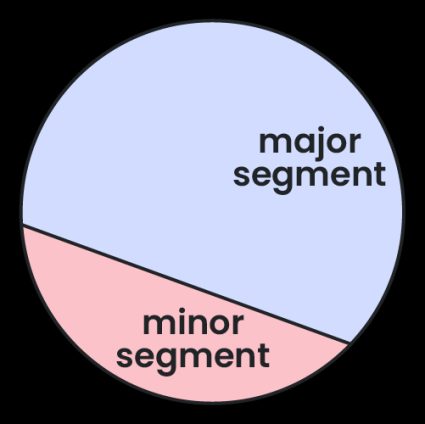
Have a look at the picture below to help you visualize the difference between segment and sector, as those two names are sometimes confused:

What is a chord of a circle?

A chord is a line that connects two points on a circle. The infinite line extension of a chord is called a secant. The special case of a chord is one that passes through the center of a circle – and that's the circle diameter, of course!
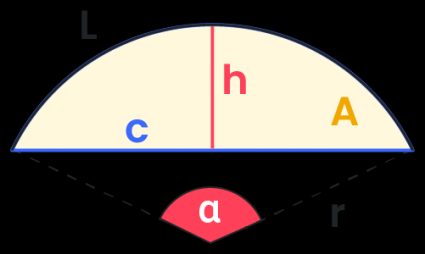
Formulas for a segment of a circle area
To find the circle segment area, you need to know at least two variables. In our segment area calculator, you'll find two popular formulas implemented:
-
Formula given radius and central angle
Asegment = 0.5 × r² × (α – sin(α))
Where does this formula come from? You can look at the segment area as the difference between the area of a sector and the area of an isosceles triangle formed by the two radii:
Asegment = Asector - Atriangle
Knowing the sector area formula:
Asector = 0.5 × r² × α (learn more about this in the sector area calculator)
An equation for the area of an isosceles triangle, given arm and angle:
Aisosceles triangle = 0.5 × r² × sin(α) (learn more about this in the isosceles triangle area calculator).
You can find the final equation for the segment of a circle area:
Asegment = Asector - Aisosceles triangle = (0.5 × r² × α) - (0.5 × r² × sin(α)) = 0.5 × r² × (α – sin(α))
-
Formula given radius and height
Asegment = r² × arccos((r-h)/r) - (r-h) × √(2 × r × h - h²)
where h is the height of a segment, also known as sagitta.
This formula may be useful when you need to calculate, e.g., the volume of water in a pipe that is not completely full.
This segment area calculator can work as a chord length calculator as well!
Let's find out how to use this segment area calculator. In our example, we want to find the area of the cross-section of a partially filled pipe:
- Input the circle radius. Assume our pipe radius is 5 in.
- Enter the second variable. Let's say that it's filled 3 inches high, so input that value into the
heightbox. - There you go, that's it! Now we know that our segment area is equal to 19.8 in². Additionally, we determined the chord length (9.17 in), arc length (11.6 in), and central angle (132.84°).
FAQs
Why might one need to calculate the area of a segment?
Calculating the area of a segment is often needed in fields like engineering, architecture, and various forms of structural design.
How do I calculate the segment area?
You can calculate the segment area in three steps:
-
Determine the radius of the circle.
-
Calculate the central angle.
-
Apply the segment area formula:
0.5 × r² × (α – sin(α))
What is the segment area if the circle has a 5 cm radius?
Assuming the height is 2 cm, the segment area will be 11.18 cm². You can calculate it using this formula:
r² × arccos((r-h)/r) - (r-h) × √(2 × r × h - h²)
What is the difference between a minor segment and a major segment?
A minor segment is smaller than a semicircle, while a major segment is larger. The difference is based on whether the central angle is less or more than 180 degrees.