Torus Volume Calculator

The torus volume calculator will determine the volume of a torus for a given pair of radii. Ever wondered what the volume is of your doughnut or ring? The bicycle you ride also run because of a couple of tori. Read on to understand what is a torus and how to calculate the volume of torus.

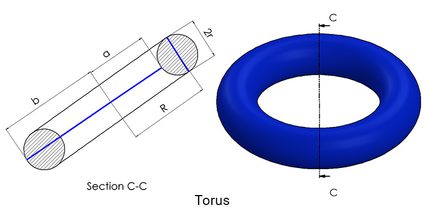
A torus is a 3D shape obtained by revolving a circle around an axis. This shape is commonly found in doughnuts, rings, tires, tubes, etc. If you take a ring and circularly trace it around with a pencil, you get a torus. In modern design software, it is fairly easy to draw them by using a revolve command with a circle as a cross-section. A torus has two radii – the first radius is the radius of the cross-section r and the second radius is the distance between the center of the torus to the center of the cross-section R.

Based on the combinations of the two radii, we can obtain multiple types of tori. Such that:

• Ring type (R > r)
• Horn type (R = r)
• Spindle type (R < r)

In addition to the these radii, the torus can also be expressed in the form of two radii such as inner (a) and outer radii (b) of the torus. Mathematically, that is:

a = R - r
b = R + r

The volume V of the said torus is:
V = 2 * π² * r² * R
The volume can also be written in terms of the inner and outer radii:
V = 0.25 * π² * (b - a)² * (b + a)
The above equation is used in the calculator as the volume of torus formula where:

• r = (b - a) / 2
• R = (a + b) / 2

What about its surface area? Check the torus surface area calculator to find out! You can then calculate the surface area to volume ratio.

Note: This calculator is only applicable to ring-type or horn-type tori. Also, in the case of a horn-type torus, i.e., R = r, minor radius, a becomes zero.

Follow three simple steps to find the volume of a torus.

• Step 1: Enter the inner radius of torus, a.
• Step 2: Enter the outer radius of torus, b.
• The calculator will now use the volume of torus formula to return the result.

Find the volume of torus having the radius of cross-section as 40 mm, and the distance from the center of torus to the center of cross-section as 100 mm.

Given: radius of cross-section, r = 40 mm; radius of torus, R = 100 mm;

Let us first convert the radii into the inner and outer radius, a and b.

a = R - r = 60 mm
b = R + r = 140 mm

• Step 1: Enter the inner radius of torus, a = 60 mm.
• Step 2: Enter the outer radius of torus, b = 140 mm.
• Step 3: Using volume of torus formula,

V = 0.25 * π²> * (b - a)² * (b + a)
V = 0.25 * π² * (140 - 60)² * (140 + 60) = 3158273 mm³
You can convert this large number to a different unit using our volume converter.
If you are done with the volume of a torus, hop over to the volume calculator to find this quantity for other various shapes, such as a capsule or a conical frustum.