Omni Calculator logo
Last updated:

Similar Triangles Calculator

New

Table of contents

What are similar triangles?Finding similar triangles: Law of similar trianglesHow do you find the missing side of a similar triangle?How do you find the area of a similar triangle?How to use this similar triangles calculatorFAQs

This similar triangles calculator is here to help you find a similar triangle by scaling a known triangle. You can also use this calculator to find the missing length of a similar triangle!

Stick around and scroll through this article as we discuss the laws of similar triangles and learn some fundamentals:

  • What are similar triangles?
  • Finding similar triangles: How do you determine whether two triangles are similar?
  • How do you find the missing side of a similar triangle?
  • How do you find the area of a similar triangle?

What are similar triangles?

Two triangles are similar if their corresponding sides are in the same ratio, which means that one triangle is a scaled version of the other. Naturally, the corresponding angles of similar triangles are equal. For example, consider the following two triangles:

The sides of ΔABC and ΔDEF are proportional
The sides of △ABC\triangle \text{ABC} and △DEF\triangle \text{DEF} are proportional.

Notice that the corresponding sides are in proportion:

DEAB=EFBC=DFAC=2\frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC}} =\frac{\text{DF}}{\text{AC}} = 2

Therefore, we can say △ABC\triangle \text{ABC} ∼\sim △DEF\triangle \text{DEF}. Here the symbol ∼\sim indicates that the triangles are similar.

We term the proportion of similarity as the scale factor (k)(k). In the example above, the scale factor k=2k = 2. If you need help finding ratios, use our ratio calculator.

Finding similar triangles: Law of similar triangles

We know that two triangles are similar if either of the following is true:

  • The corresponding sides of the triangle are in proportion; or
  • The corresponding angles are equal.

From this, we can derive specific rules to determine whether any two triangles are similar:

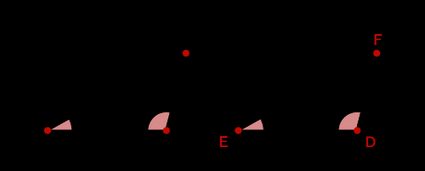
  1. Side-Side-Side (SSS): If all three corresponding sides of the two triangles are in proportion, they are similar. This rule is the most straightforward and requires you to know all the sides of the triangles.
The sides of $$\triangle \text{ABC}$$ and $$\triangle \text{DEF}$$ are proportional.
All sides of the triangles △ABC\triangle \text{ABC} and △DEF\triangle \text{DEF} must be known and proportional to each other.

We can express this using a similar triangle formula:

DEAB=EFBC=DFAC=k\qquad \frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC}} =\frac{\text{DF}}{\text{AC}} = k

where kk is the scale factor.

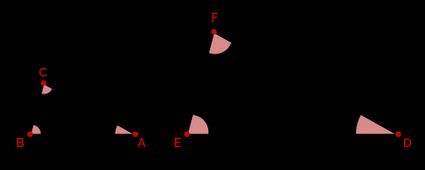
  1. Side-Angle-Side (SAS): If any two corresponding sides of two triangles are in proportion and their included angles are equal, then the triangles are similar. We can use this rule whenever we know only two sides of each triangle and their included angles.
SAS similarity criterion.
Any two pairs of sides must be in proportion and their inscribed angles must be equal.

The triangles in the image above are similar if:

DEAB=DFAC=k,and∠BAC=∠EDF\qquad \begin{align*} &\frac{\text{DE}}{\text{AB}} = \frac{\text{DF}}{\text{AC}} = k, \text{and}\\\\ & \angle\text{BAC} = \angle\text{EDF} \end{align*}

This rule is handy in cases like in the image below, where the triangles share an angle:

Two triangles with a common vertex (shared angle).
The triangles △ABC\triangle \text{ABC} and △PBQ\triangle \text{PBQ} share an angle. It is easier to check for SAS criterion in such cases.

You can do many things knowing just the Side-Angle-Side of a triangle. Learn more using our SAS triangle calculator.

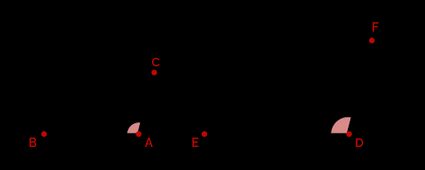
  1. Angle-Side-Angle (ASA): If any two corresponding angles of two triangles are equal and the corresponding sides between them are in proportion, the triangles are similar.
Two triangles with two pairs of equal angles and the corresponding side pair in proportion.
Two triangles with two pairs of equal angles are similar. Knowing the corresponding sides will help determine their scale factor.

The triangles in the image above are similar if:

∠BAC=∠EDF,∠ABC=∠DEF, andDEAB=k\qquad \begin{align*} & \angle\text{BAC} = \angle\text{EDF}, \\ & \angle\text{ABC} = \angle\text{DEF}, \text{ and}\\\\ &\frac{\text{DE}}{\text{AB}} = k \end{align*}

You can find the third angle if you know any two angles in a triangle using our triangle angle calculator. We know that if any two corresponding angles in the triangles are equal, the triangles are similar, meaning that in the ASA congruence rule, we don't need to know the side so long as the angles are known. However, without the sides, we cannot determine the scale factor kk.

💡 Need to find the area of a triangle? We have our triangle area calculator that can help you with that.

How do you find the missing side of a similar triangle?

To find the missing side of a triangle using the corresponding side of a similar triangle, follow these steps:

  1. Find the scale factor k of the similar triangles by taking the ratio of any known side on the larger triangle and its corresponding side on the smaller one.
  2. Determine whether the triangle with the missing side is smaller or larger.
  3. If the triangle is smaller, divide its corresponding side in the larger triangle by k to get the missing side. Otherwise, multiply the corresponding side in the smaller triangle by k to find the missing side.

For example, consider the following two similar triangles.

Two similar triangles $$\triangle \text{ABC}$$ and $$\triangle \text{DEF}$$ where the side $$\text{AC}$$ is unknown.
Two similar triangles △ABC\triangle \text{ABC} and △DEF\triangle \text{DEF} where the side AC\text{AC} is unknown.

To find the missing side, we first start by calculating their scale factor.

k=DEAB=84=2k = \frac{\text{DE}}{\text{AB}} = \frac{8}{4} = 2

Next, we use the scale factor relation between the missing side AC and its corresponding side DF:

DFAC=k=2AC=DF2=62AC=3\begin{align*} \frac{\text{DF}}{\text{AC}} &= k=2\\[1em] \text{AC} &= \frac{\text{DF}}{2} = \frac{6}{2}\\[1em] \text{AC} &= 3 \end{align*}

🙋 You can also compare two right triangles and see their similarities using our Check Similarity in Right Triangles Calculator.

How do you find the area of a similar triangle?

To find the area of a triangle A1 from the area of its similar triangle A2, follow these steps:

  1. Find the scale factor k of the similar triangles by taking the ratio of any known side on the larger triangle and its corresponding side on the smaller one.
  2. Determine whether the triangle with the unknown area is smaller or larger.
  3. If the triangle is smaller, divide A2 by the square of the scale factor k to get A1 = A2/k2. Otherwise, multiply A2 by k2 to get A1 = A2 × k2.

How to use this similar triangles calculator

Now that you've learned how to find the length of a similar triangle, the similar triangles formula, and more, you can quickly figure out how this similar triangles calculator works.

To check whether two known triangles are similar, use this calculator as follows:

  1. Select check similarity in the field Type.
  2. Choose the similarity criterion you want to use. You can choose between Side-Side-Side, Side-Angle-Side, and Angle-Side-Angle.
  3. Enter the dimensions of the two triangles. The calculator will evaluate whether they are similar or not.

To use this calculator to solve for the side or perimeter of similar triangles, follow these steps:

  1. Select find the missing side in the field Type.
  2. Enter the known dimensions, area, perimeter, and scale factor of the triangles. The similar triangles calculator will find the unknown values.
FAQs

Are all equilateral triangles similar?

Yes, if the corresponding angles of two triangles are equal, the triangles are similar. Since every angle in an equilateral triangle is equal to 60°, all equilateral triangles are similar.

Find the scale factor of similar triangles whose areas are 10 cm² and 20 cm²?

1.414. To determine this scale factor based on the two areas, follow these steps:

  1. Divide the larger area by the smaller area to get 20/10 = 2.
  2. Find the square root of this value to get the scale factor, k = √2 = 1.414.
  3. Verify this result using Omni's similar triangles calculator.
Least Common Multiple CalculatorAbsolute Value CalculatorInterval Notation CalculatorLeast Common Denominator CalculatorNull Space CalculatorTrig Identities CalculatorPartial Fraction Decomposition CalculatorUnit Rate CalculatorExponential Function Calculator
Check out 19 similar triangle calculators 🔺
30 60 90 triangle45 45 90 triangleArea of a right triangle...16 more