Secant Calculator

Welcome to Omni's secant calculator (or sec calculator, if you prefer), where we'll study the mysterious sec function. Arguably, it is one of the lesser-known functions in trigonometry, but it can still prove useful. We will not only give the secant definition, i.e., the secant formula, but we'll also discuss what the domain of secant is, give the sec graph, and explain how to find the secant using alternative methods.

"So what is this secant equal to?" Well, why don't we move to the first section and find out?

All of trigonometry begins with a right triangle (you know, one of those that the Pythagorean theorem is about). Trigonometric functions, such as the one in our sec calculator, are a tool to describe the correspondences between a triangle's sides. Below you can find how we obtain them. In particular, we have there the secant definition.

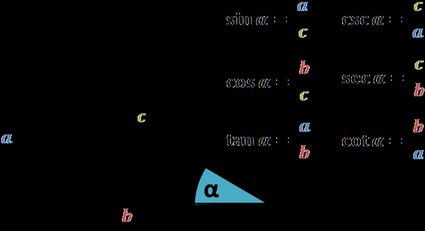
So what is secant equal to? According to the picture above, the secant formula is: to divide the hypotenuse by the side next to the angle.

A keen eye will observe that we have no information about the size of the triangle. That is precisely the magic behind trigonometric functions such as sec in math: even if we scale the triangle to a different size, as long as the angle stays the same, the value of the function will not change.

Despite this advantage, there is a slight drawback here. With the sec trig function defined this way (and all the other functions, for that matter), we can only have an angle between $0$ and $90$ degrees (or between $0$ and $\pi/2$ in radians) simply because it's a right triangle. There is, however, a way to extend the whole thing to any real angle, even a negative one. The trick is to translate the secant definition and formula into a two-dimensional Euclidean space, i.e., a plane.

Let $A = (x,y)$ be a point on the Euclidean plane and denote by $\alpha$ the angle going counterclockwise from the positive half of the horizontal axis and the line segment connecting $(0,0)$ and $A$. (Observe how we said that $\alpha$ goes from one line to the other and not that it is between them. Because of that, we often call $\alpha$ a directed angle.)

Clearly, such an angle can be larger than $90$ degrees. Even better – it can be larger than the full $360$ degrees: it can make one full circle and, from $360\degree$ upwards, begin its second lap. Also, since we've defined $\alpha$ to be directed, we can now have negative angles by simply going the other way, i.e., clockwise instead of counterclockwise.

For such angles, we extend the definitions of trigonometric functions from above by substituting in the formulas above $a$ for $y$, $b$ for $x$, and $c$ for $\sqrt{x^2+ y^2}$ (the distance from $(0,0)$ to $A$). So what is sec in this new language? Comparing the new variables with the secant formula we had above, we obtain:

Lucky for us, the secant definition was the last bit of theory we need. From now on, we'll focus on analyzing the function and listing some of its properties. We begin with drawing and taking a closer look at the sec graph.

You might have already seen the graph of sine or that of tangent since they are among the most commonly used trigonometric functions. The sec graph, however, is rarely shown at school, and it's a real pity because it's quite funky, to say the least.

Without further ado, here it is (note that we can find the same picture in our secant calculator):

From the sec graph alone, we can read off a few useful properties of the function.

• The value of the secant function is either smaller or equal to $-1$, or larger or equal to $1$. If you prefer, we can say equivalently that its absolute value is at least $1$.

• The secant function is even. This means that the value at angle $\alpha$ is the same as that at angle $-\alpha$, i.e., that $\sec(\alpha) = \sec(-\alpha)$. Visually, this means that the sec graph has a vertical axis of symmetry going through the point $(0,0)$.

• The sec trig function is periodic with a $360$-degree period. This characteristic means that the function's values repeat every $360$ degrees. In mathematical notation, we can write this fact as $\sec(x) = \sec(x + 360\degree)$.

• Similarly to the tangent, the sec trig function doesn't always exist: try our tangent calculator to see how. For the angle equal to $90\degree + k\cdot180\degree$ with $k$ an integer, the secant is not defined. On the sec graph, this translates to the function going to plus/minus infinity at these points.

Let us commit a few more lines to the last property above. Since our function is undefined at some points, those points do not belong to the domain of the secant. All in all, just to have a taste of good ol' mathematical notation, we can write:

where $\mathbb{D}(\sec)$ denotes the domain of the secant function. And in normal language, this just means it consists of all the points that are not of the form $90\degree + k\pi$ with $k$ an integer.

Alright, we're beginning to get to know each other better, my dear secant function! It's not yet the time to ask it out on a date, but we might be getting there in the long run.

So far, we've learned how to find the secant using the sides in a triangle or the coordinates of Euclidean space. It's time to leave the graph aside and look at the function algebraically. This way, we'll be able to relate the mysterious sec that math rarely uses to other maps that are far more common.

What is secant equal to? We've already seen in the first section that in a right triangle, it's the hypotenuse divided by the side next to the angle. In general, i.e., in the Euclidean plane, it's the distance from a given point to $(0,0)$ divided by the $x$ coordinate of that point.

However, since sec in math is arguably not the most common trigonometric function, maybe we can somehow relate it to some of the other ones, that you can meet at our trigonometric functions calculator?

Indeed, we can. First of all, observe that the lengths mentioned in the secant definition in the first section are also used to define the cosine; it's just that the sec function has them reversed. This gives us a nice trigonometric identity:

Or, if you prefer fractions,

Note, however, that this does not mean that secant is the inverse function to cosine. That would be arccos, which returns an angle corresponding to a value. So what is sec, then? It is the inverse of $\cos(x)$. Although it sounds very similar, it's quite a different thing than an inverse function. To clear the confusion, visit the cosine calculator and the tool related to its inverse function, the arccos calculator.

Now, we can use this new secant formula to develop yet another one. If we recall the identity $\tan(x) = \sin(x) / \cos(x)$, then we can write:

We could play around like this with the functions all day, but time is money, they say (or at least that's what the time value of money formula tells us!). Instead, let's leave the technical mumbo-jumbo behind and move on to some examples that actually have numbers in them.

Shall we?

Say that you have a trigonometry test coming soon, and you sit down at your desk to study a bit. To get a good grip on the functions, you decide to calculate their values for a few different angles: $30\degree$, $45\degree$, $60\degree$, and $75\degree$. Needless to say, we'll focus on how to find the secant.

First of all, let's see how easy the task is when we have Omni's secant calculator at hand. In it, we only have one variable field: the angle. Once we input the value, the answer appears underneath, so all we have to do is write the angles one by one and read off the values. Observe how for the first two, the secant calculator also gives precise values before rounding them up, i.e., in the form of a fraction with square roots. We will describe the reason behind it shortly.

Still, let us also try to find the answer ourselves using all that we've learned today.

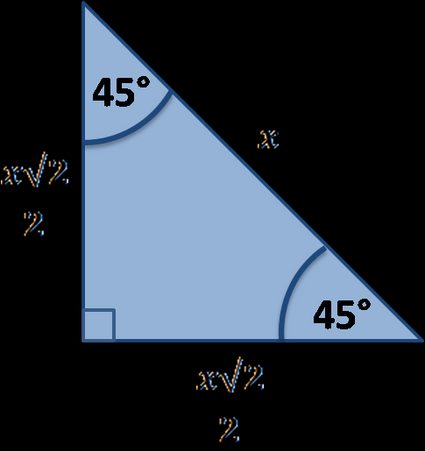
First of all, let's draw an example of a triangle with one angle equal to $30\degree$:

Note that it is an example of quite a special right triangle (yup, we call them like that: see our special right triangles calculator), in which we know the relation between its sides, i.e., that if one side is equal to $x$, then the other two are $2x$ and $x\sqrt{3}$. Also, observe that we can use the same picture for the $60\degree$ angle.

Recall from the first section that sec is a trig function obtained by dividing the hypotenuse by the side next to the angle. If we apply it to our case, we'll get:

And:

Now, that wasn't so hard, was it? Encouraged, we move on to the $45\degree$ case. Again, we begin with a picture.

We repeat the reasoning above and obtain the following:

Lastly, we have the $75\degree$ angle. Here, however, there is no nice triangle that we could work with. We could, for instance, observe that $75$ is half of $150$. Furthermore, since $180 - 150 = 30$, it shouldn't be too difficult to find $\cos(150\degree)$, which we could use to find $\cos(75\degree)$ using the half-angle formulas. Lastly, we would take the alternative secant formula from the above section and eventually get $\sec(75\degree)$.

The lesson here is that, in general, finding the values of trigonometric functions is no walk in the park. It is often best to use an external tool for that, and oh, how lucky we are that we have the Omni website to provide just that!

All in all, you can feel ready for the upcoming test! Do you think they'll increase the classroom spacing for it to further discourage cheating?