Right Trapezoid Area Calculator

Q: How to find the area of a right trapezoid

To find the area of a right trapezoid, use the formula: A = ( a + b ) x h/2 . Where: A – Area of the trapezoid; a and b – Bottom and top bases; and h – The height.

Q: Can a trapezoid have exactly one right angle?

No, a trapezoid can't have only one right angle. The minimum amount of right angles a trapezoid can have is two. This configuration is known as a right trapezoid. The following number of right angles is four; this is the case of a rectangle.

Q: How do I find the height of a right trapezoid?

To find the height of a right trapezoid you might meet one of these cases: If the bases a and b , and the slant side d are known, use the Pythagorean theorem: h = √(d² - (a - b)²) . When knowing the slant side d and the acute angle δ use: h = arcsin(δ) x d . If knowing the slant side d and the obtuse angle γ utilize: h = arcsin(γ - π/2) x d .

Creators

Gabriela Diaz

Gabriela Diaz is a Mechanical Engineer with a blend of industry and academic experience. She has contributed to oil and gas projects in Venezuela and served as a professor of mechanics at Simón Bolívar University. Her professional work includes managing piping materials inventory, designing pressure vessels, and conducting research in thermoeconomic analysis to optimize resource use and minimize waste in oil facilities. Beyond her engineering career, Gabriela has also been involved in her family’s fashion business. In her free time, you might find her training for local running competitions, learning to play the guitar, and exploring new languages. See full profile

Check our editorial policy

Reviewers

Luciano Miño

A physics student, self-taught web developer, and data scientist, Luciano is extremely curious and passionate about problem-solving and programming. He’s always eager to learn new things that allow him to get a deeper understanding of the problem at hand and produce the most simple yet complex answer to any given situation, making calculator-building his natural habit. His experience teaching Math and Physics to high school and college students allows him to write clear and understandable texts that approach the reader in a friendly manner. In his free time, he enjoys weightlifting, meditation, and tackling new programming projects. See full profile

Check our editorial policy

New

Welcome to the right trapezoid area calculator, where you'll be able to compute the area of any right trapezoid in a blink of an eye! 😉
Here we'll also learn:

What is a right trapezoid; and
How to find the area of a right trapezoid yourself, even if at first you don't know its height.

Shall we get started?

What is a right trapezoid?

A right trapezoid is a particular case of a trapezoid, a four-sided geometry with at least one pair of opposite sides parallel to each other. These parallel sides, also known as bases, are identified in the image below as $a$ and $b$ .

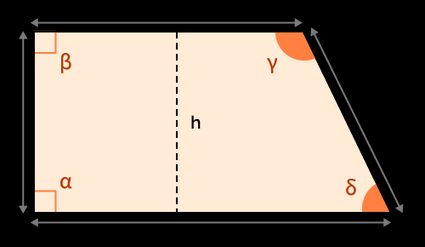
In the specific case of a right trapezoid, one of the two remaining sides, $c$ from the figure, is perpendicular to the parallel sides $a$ and $b$ , creating 90° angles (right angles) between them.

How to find the area of a right trapezoid

To find the area of a right trapezoid, use the formula: A = ( a + b ) x h/2.

Where:

A – Area of the trapezoid;
a and b – Bottom and top bases; and
h – The height.

Meaning that if you know all of these dimensions, you'll be able to calculate the area of your right trapezoid directly.

But what if you don't know the height h? Would you still be able to calculate the area? This is when some good old trigonometry comes to the rescue!

Looking at the image, we can see a right triangle forming from the height h, the difference of the bases (a - b) and the side d.

From here, if you know:

The two sides (a - b) and d; or
One side and one angle of the right triangle, you're all set!

If you know two sides, the calculation of h revolves around the Pythagorean theorem as:

h = √(d² - (a - b)²)

On the other hand, if you have one side and one angle, you can get the value of h by using the arcsine function (the inverse of the sine) as:

h = arcsin(δ) * d

or...

h = arcsin(γ - π/2) * d

💡 You can learn more about the arcsine trigonometric function with our arcsin calculator. For other trigonometric functions, check our trigonometry calculator!

How to use the right trapezoid area calculator

To use the right trapezoid area calculator:

Input the bases a and b. For example, let's assume a = 10 and b = 6.
Enter the value of the height h. In our example, suppose h = 4.
The calculator will display the result for the area on the last row. For our calculation, we get A = 32. And that's it! 😀

💡 If, instead, you don't know the value of the height h, you can click on the Angles and slant side section to obtain it by entering the angles and the slant side.

More trapezoid calculators

Now that you've learned how to calculate the area of a right trapezoid, why not read about the area of an irregular trapezoid or ultimately expand your knowledge about trapezoids with our trapezoid calculator.

To learn about specific topics concerning trapezoids, we recommend other of our tools:

FAQs

Can a trapezoid have exactly one right angle?

No, a trapezoid can't have only one right angle. The minimum amount of right angles a trapezoid can have is two. This configuration is known as a right trapezoid. The following number of right angles is four; this is the case of a rectangle.

How do I find the height of a right trapezoid?

To find the height of a right trapezoid you might meet one of these cases:

If the bases a and b, and the slant side d are known, use the Pythagorean theorem: h = √(d² - (a - b)²).
When knowing the slant side d and the acute angle δ use: h = arcsin(δ) x d.
If knowing the slant side d and the obtuse angle γ utilize: h = arcsin(γ - π/2) x d.