Right Cylinder Calculator: find A, V, A_l, A_b
The right cylinder calculator is an advanced tool that finds the area, volume, lateral area, and base area of a right cylinder. Enter some of your selected values to calculate other parameters, or keep reading the article below to learn about all the equations we have used. The notation is as follows:
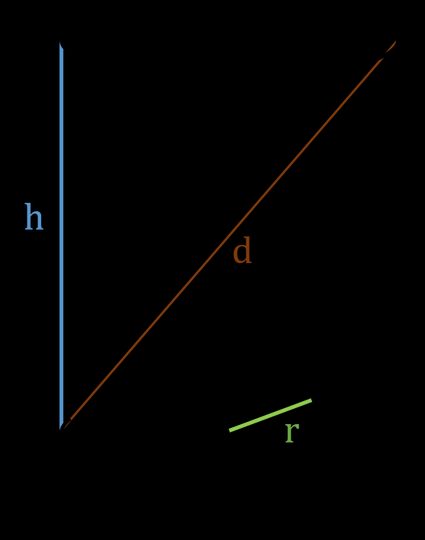
- r — Radius of a circle (base);
- h — Height of a cylinder;
- A — Total surface area of a cylinder (right cylinder calculator: find A);
- V — Volume of a cylinder (right cylinder calculator: find V);
- A_l — Lateral surface area of a cylinder (right cylinder calculator: find A_l);
- A_b — Base surface area of a cylinder (right cylinder calculator: find A_b);
- d — Longest diagonal of a cylinder; and
- A / V — Surface-to-volume ratio of a cylinder.
A cylinder is a three-dimensional solid with two congruent parallel planes called bases of the cylinder. It consists of all the points on all the lines that connect its bases. A cylinder is right when one base lies exactly above the other. Otherwise, it is called an oblique cylinder. If the bases are circles, then the cylinder is called a circular cylinder. Remember that traditionally, the term cylinder usually refers to the right circular cylinder — our right cylinder calculator is dedicated to this type of cylinder.
You should also check out our cylindrical coordinates calculator and see how you can use a cylinder to describe the position of any given point in a 3D space.
Right cylinder calculator: find A_b
The base surface area of a right circular cylinder A_b is simply the sum of the areas of two bases. Its value is expressed in squared units of length, e.g., square meters m² or square feet ft². Check out area conversion calculator to learn how to convert between different area units! Because both bases of a right circular cylinder are the same circles with the radius r, the base surface area of a cylinder is two times the area of a circle:
a_b = 2 × π × r²
But what if you don't know the radius of the base? There are several different ways to estimate the base surface area of a cylinder:
-
With given total area and lateral area:
A_b = A − A_l -
With given volume and height:
A_b = 2 × V / h -
With given lateral area and height:
A_b = A_l²/(2 × π × h²) -
With given longest diagonal and height:
A_b = π/2 × (d² − h²)
Right cylinder calculator: find A_l
To find the lateral surface area of a right circular cylinder A_l, we open the cylinder like a carton box and flatten it out to find out which geometric figures it contains – this is the so-called net of a solid. As you can see below, a right circular cylinder consists of two circles (bases) and one rectangle (lateral surface).
The first side of that rectangle is the height h of the cylinder, and the second side equals the circumference of the base – 2 × π × r (circle with radius r), as shown in the circumference calculator. Therefore, the lateral surface area of a right circular cylinder A_l can be found just like the area of a rectangle:
A_l = 2 × π × r × h
There are also other equations that lead to the lateral surface area of a cylinder:
-
With given total area and base area:
A_l = A − A_b
-
With given volume and height:
A_l = √(4 × π × h × V)
-
With given base area and height:
A_l = √(2 × π × h² × A_b)
-
With given longest diagonal and height:
A_l = √(d²h²π² − h⁴π²)
If you need to make several calculations with rectangles, then our area of a rectangle calculator might be the right tool to check!
Right cylinder calculator: find A
The total surface area of a right circular cylinder A is the sum of all the areas of the faces that a cylinder has, i.e., a top base, a bottom base, and a side. Therefore, the total surface area of a right circular cylinder is the sum of its base surface area A_b and its lateral surface area A_l:
A = A_b + A_l = 2 × π × r² + 2 × π × r × h
and after some trivial simplification
A = 2 × π × r × (r + h)
Right cylinder calculator: find V
The volume of a right circular cylinder V is the space enclosed by a cylinder. Its value is expressed in cubic units of length, e.g., cubic meters m³ or cubic feet cu ft. Try our volume conversion to learn how to convert between different volume units! The volume of a right circular cylinder is a product of the height h and the area of one base A_b/2 = π × r². Thus, it can be found with the following equation:
V = A_b/2 × h = π × h × r²
It is worth remembering that this formula holds whether or not the cylinder is a right cylinder – it is also true for oblique cylinders. In the case of a right circular cylinder, you can also use other formulas to estimate the volume of a cylinder:
-
With given lateral area and height:
V = A_l² / (4 × π × h) -
With given lateral area and radius:
V = A_l × r / 2 -
With given base area and lateral area:
V = √(A_l² × A_b / (8 × π)) -
With given longest diagonal and height:
V = (π × h × d² − π × h³)/4
