Area of a Rectangle Calculator

Whether you need to know the area of a carpet, a parcel, a TV screen, a rectangle pool, or a window, this area of a rectangle calculator will solve your problem in a blink of an eye!

All you have to do is input the length and width (or diagonal) and allow this rectangle calc to find the values of P (perimeter) and A (area).

Keep reading if you want to understand what a rectangle is, you're interested in the rectangle definition, formulas, and properties of a rectangle... Or you just want to learn how to find the area of a rectangle.

A rectangle is a quadrilateral with four right angles. We may also define it in another way: a parallelogram containing a right angle – if one angle is right, the others must be the same. Moreover, each side of a rectangle has the same length as the one opposite to it. The adjacent sides need not be equal, in contrast to a square, which is a special case of a rectangle.

If you know some Latin, the name of a shape usually explains a lot. The word rectangle comes from the Latin rectangulus. It's a combination of rectus (which means "right, straight") and angulus (an angle), so it may serve as a simple, basic definition of a rectangle.

A rectangle is an example of a quadrilateral. You can use our quadrilateral calculator to find the area of other types of quadrilateral.

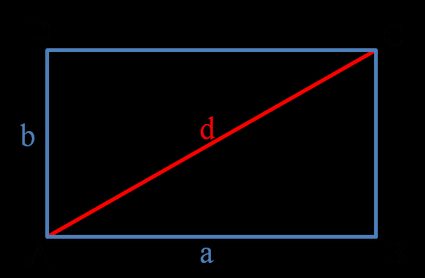
The image above shows a typical rectangle. It has four sides and four right angles. The lengths of its sides are denoted with a and b, while the length of the diagonal is denoted with d.

If all sides of the rectangle have equal lengths, we call it a square.

The area of a rectangle is a space restricted by its sides or, in other words, within the perimeter of a rectangle. To find the area of a rectangle, all you need to do is a multiplication of rectangular sides a and b:

Area = a × b

Our rectangle calculator has the following formulas implemented:

• For the area of a rectangle:
  A = a × b

• For the perimeter of a rectangle:
  P = 2 × (a + b)

• For the diagonal of a rectangle:
  d² = a² + b²
d = √(a² + b²)

As we know the formula for the area of a rectangle A = a × b, let's show with an example how you can calculate that property:

1. Choose the length of the rectangle – for example, a = 5 cm.
2. Decide on the rectangle's width – for example, b = 6 cm.
3. Multiply these two values: A = 5 cm × 6 cm = 30 cm².
4. The area of the rectangle is 30 cm².

Let's find out how to find the perimeter of a rectangle. As usual, the perimeter is a sum of all sides of a shape:

P = a + b + a + b

...which can be written as:

P = 2 × (a + b)

Let's take the same rectangle as an example:

1. Choose the length of the rectangle – a = 5 cm in our case.
2. Decide on the width of the rectangle – e.g., b = 6 cm.
3. Add these two values: a + b = 5 + 6 = 11 cm.
4. Multiply the result by 2: P = 2 × 11 = 22 cm.
5. Here we go! The perimeter of our rectangle is 22 cm.

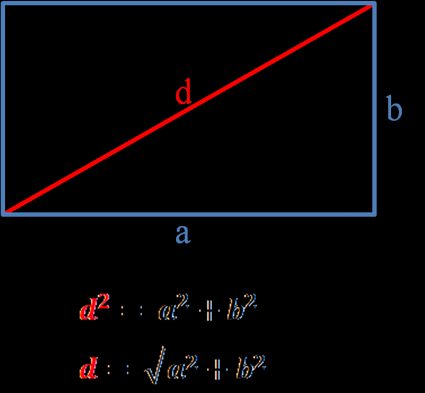
The diagonal of a rectangle is a segment that connects two opposite vertices of a rectangle. Let's calculate the diagonal length of the exemplary rectangle:

1. Choose the length of the rectangle – for example, a = 5 cm.
2. Decide on the rectangle's width – for example, b = 6 cm.
3. Calculate a to the power of two: a² = 25 cm².
4. Calculate b to the power of two: b² = 36 cm².
5. Add these two values: a² + b² = 25 + 36 = 61 cm².
6. Finally, take the square root of the result: d = √(a² + b²) = √61 ~ 7.81 cm.
7. The length of the diagonal is 7.81 cm.

Naturally, instead of calculating all of these values manually, you can use this area of a rectangle calculator. You can also use it in reverse – for example, to calculate the width of a rectangle with a known length and perimeter.

The figure above shows a special type of rectangle called the golden rectangle (learn with our golden rectangle calculator). Such a rectangle fulfills the following condition:

(a + b) / a = a / b = ϕ

where φ is the golden ratio equal to 1.618. Find out more about this special ratio with our golden ratio calculator.

As you probably remember from the ratio calculator, a ratio is a relationship between two quantities, often represented as a fraction.

Did you know that you can construct the golden rectangle using only a straightedge and compass? It's just a few steps!

1. Draw a square.
2. Draw a line from the midpoint of one side of the square to the opposite corner. Our midpoint calculator can help you with this step.
3. Draw a circle with a radius equal to that line and center in the midpoint, as in the picture above.
4. The point where the circle meets the extended square side is the next corner of the golden rectangle.
5. Find the last vertex and complete the golden rectangle.

Taadaaah! It wasn't so hard, was it?

Rectangles have many interesting properties:

• Cyclic – meaning that all corners lie on a single circle.
• Equiangular – all its corner angles are equal to 90 degrees.
• Rectilinear – its sides meet at right angles.
• Two lines of reflectional symmetry – vertical and horizontal through the center.
• Two diagonals, which bisect each other. You can find the diagonal length using the Pythagorean theorem.
• Opposite sides of a rectangle are parallel to each other and have equal lengths.

Other lesser-known rectangular properties:

• The intersection of the diagonals is the circumcenter – a circle exists which has a center at that point, and it passes through the four corners.
• In a rectangle with different side lengths (simply speaking – not a square), it's not possible to draw the incircle.
• Lines joining the midpoints of the sides of a rectangle form a rhombus, which is half the area of the rectangle. The sides of the shape are parallel to the diagonals.

You can think of your own properties as well, e.g., concerning the revolution of a rectangle – along the side or diagonal to get a cylinder or a cone, respectively.

TL;DR:

1. Is a square a rectangle? YES.
2. Is a rectangle a parallelogram? YES.
3. Is a rectangle a rhombus? In general – NO. Only if it's a square (the angles of the rhombus are all 90 degrees).
4. Is a rhombus a rectangle? In general – NO. Only if it's a square (the sides of the rectangle are all equal in length).
5. Is a rectangle a quadrilateral? YES, of course.
6. Is a rectangle a trapezoid? YES.

Wondering if a square is a rectangle or if a rectangle is a parallelogram? Have a look at the picture below, and you shouldn't have any doubts about the relations between quadrilaterals anymore:

How to read this diagram? Let's start with our rectangle. Three figures are connected directly to the shape: a square, a parallelogram, and an isosceles trapezoid. So if the shape is above our shape of interest – like square and rectangle – we can say that:

• Every square is a rectangle and a square is a special case of a rectangle.

For the other two figures, we can state analogically:

• Every rectangle is a parallelogram and a rectangle is a particular case of a parallelogram.
• Every rectangle is a trapezoid and a rectangle is a special case of a trapezoid.

Many different rankings exist, evaluating the countries – whether by their areas, populations, level of education, or Nobel prize winners.

But have you ever wondered who's the winner of the most rectangular country competition? An Australian geo-statistician David Barry calculated the parameter of rectangularity for all countries in the world and created a ranking.

He found out that the most rectangular country is Egypt, whereas the "least rectangular country in the world" title goes to the Maldives (however, the author admits that calculations for countries that consist of many small islands could be terribly wrong). Have a look at the table below and check out the first ten countries, as well as the least rectangular ones.

Egypt is the leader, but that shouldn't surprise anybody checking the shape of that country on the map. The USA is in the middle of the ranking, mainly because of the eccentricity of Alaska and Hawaii. The confusing thing is that the 2nd most rectangular country – Vatican – is at the same time the 4th-roundest country, and Poland, 5th in roundness classification, is 9th in the rectangularity ranking.

How is it even possible to be rectangular and round at the same time?! As you can guess, it's all about the definition of rectangularity and roundness, which may not be adequate for complex or scattered shapes – and the borders of countries are usually such examples, containing sharp edges, small islands, or colonies somewhere on the other part of the globe.

If you're interested in the topic, you can have a look at this explanation and discussion of the results.

You could think that the world would be easier to draw if every country were a rectangle... Or would it?

The shape of a rectangle is used in many periodic tessellation patterns. It may be used for walls of bricks, floor tiles, pavement, or different mosaics. Below, you'll find a few popular patterns:

• Stacked bond – it's the most common and simplest tiling pattern, as tiles are laid in straight lines.

• Running bond – typical for pavements, tile, and brick bonds.

• Herringbone – wooden floors look good with this kind of pattern.

• Basketweave – often used for hallways or outdoor paths.

Of course, tiles come in all shapes and sizes – hexagonal and octagonal with squares are quite popular choices. For the pentagon, the shape must be irregular to form a tiling pattern.

Body shape type is one of the most searched-for problems connected to rectangles. All you need to do is to measure your bust, waist, hips, and high hip and type the values into the tool. Then, you'll get the information about what your body shape is.

For example, the rectangle body shape is defined as a "boyish" body type – your hips, waist, and bust are about the same size. Your body is well-proportioned and athletic in appearance.

Surprisingly, we are surrounded by rectangular objects. That's why our rectangle calculator may be useful not only for math classes but also in your everyday life problems. Of course, you won't find an ideal rectangle in reality, as it always has a third dimension; but if it's small compared to the other two measurements, the approximation is good enough.

• Rectangle tablecloths – given the size of your table, you can find out what tablecloth is needed or how much lace or hemming tape you need to use.

• Doors or window glass – did a storm or a golf ball break your window pane? Calculate the area and estimate the repair cost, given the price per sq ft or sq meter.

• Screens of electronic devices – tablets, smartphones, TVs – use this area of a rectangle calculator to estimate how much space on the wall your screen will take up – or how big the screen of the phone you want to buy is.

• Blackboards, mirrors, frames, canvas, sheets of paper, notebooks, envelopes, money, flags, rectangle pools... It's a never-ending list!

Have a look. Can you find more rectangular objects around you? Sure you can!

To find the perimeter, you need to sum up all sides of a rectangle:

P = a + b + a + b

To find the area of a rectangle, you need to multiply the shorter and longer sides:

A = a × b

It's 144 square inches! To find this rectangle's area, you need to:

1. Convert feet to inches. 3 feet is equal to 36 inches.
2. Multiply the width and length of the rectangle. The area is equal to 4 times 36.
3. Check your result in our area of a rectangle calculator!

A shape is a rectangle if:

1. It has two dimensions – length and width.
2. It has four sides that create four angles.
3. All the angles are right (90°).
4. Opposite sides of a rectangle are parallel to each other and have equal lengths.