Quadrilateral Calculator
If you are wondering how to find the area of any quadrilateral, check out this quadrilateral calculator. We implemented three quadrilateral area formulas so that you can find the area given diagonals and angles between them, bimedians and angles between them, or all sides and two opposite angles. In the default option, you can also find the quadrilateral perimeter. If you are looking for a specific quadrilateral shape - for example, a rhombus or a kite - check our comprehensive list of area calculators below.
What is a quadrilateral?
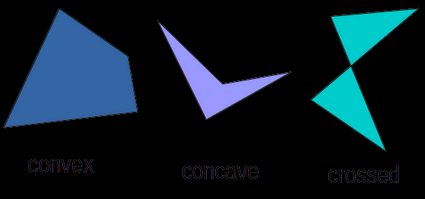
A quadrilateral is a polygon with four edges and four vertices. Sometimes it is called a quadrangle or a tetragon, by analogy to three-sided triangles and polygons with more sides (pentagon, hexagon, heptagon, octagon, etc.). Quadrilaterals can be:
- Simple (not self-intersecting)
- Convex - all interior angles < 180°, both diagonals lie inside the quadrilateral
- Concave - one interior angle > 180°, one diagonal lie outside the quadrilateral
- Crossed, also called complex, butterflies, or bow-ties (self-intersecting)
Quadrilateral shapes
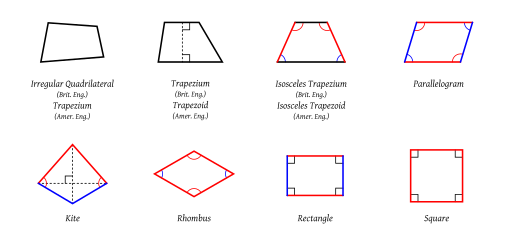
There are many types of convex quadrilaterals. The basic ones are:
- Irregular quadrilateral (UK) / trapezium (US): no sides are parallel. That's the case in which our parallelogram area calculator is particularly useful.
- Trapezium (UK) / trapezoid (US): at least one pair of opposite sides are parallel. Isosceles trapezium (UK)/isosceles trapezoid (US) is a special case with equal base angles.
- Parallelogram: has two pairs of parallel sides.
- Rhombus or rhomb: all four sides are of equal length.
- Rectangle: all four angles are right angles.
- Square: all four sides are of equal length (equilateral), and all four angles are right angles.
- Kite: two pairs of adjacent sides are of equal length.
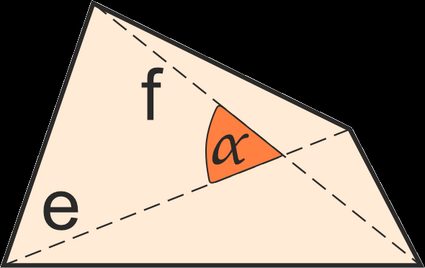
Quadrilateral area formulas
In this calculator, you can find three ways of determining the quadrilateral area:
-
Given four sides and two opposite angles:
According to Bretschneider's formula, you can calculate the quadrilateral area as:
area = √[(s - a) × (s - b) × (s - c) × (s - d) - a × b × c × d × cos²(0.5 × (angle1 + angle2))]where
a, b, c dare quadrilateral sides,sis the semiperimeter (0.5 × (a + b + c + d)), andangle1andangle2are two opposite angles. -
Given diagonals and angle between them:
area = p × q × sin(angle) / 2, wherep, qare diagonals -
Given bimedians and angle between them:
area = m × n × sin(angle), wherem, nare bimedians - lines that join the midpoints of opposite sides -
Given the Cartesian coordinates of the vertices
If we list the vertices of our quadrilateral in the counterclockwise order:
(x1, y1), (x2, y2), (x3, y3), (x4, y4)
then the shoelace formula tells us that the area of this quadrilateral is given by the following formula:
area = 0.5 × (x1y2 - y1x2 + x2y3 - y2x3 + x3y4 - y3x4 + x4y1 - y4x1)
How to find the quadrilateral area
Assume that you want to calculate the area of a parcel. It's in the quadrilateral shape, but not any specific - it's neither a rectangle nor a trapezoid. The quadrilateral area calculator is the best choice!
- Choose the option with your given parameters. The default value is the easiest to measure in the field or on the map, with 4 sides and 2 opposite angles. Let's pick that option.
- Enter the given values. For example, a = 350 ft, b = 120 ft, c = 280 ft, d = 140 ft, angle1 = 70 , angle2 = 100. Remember that you can easily change the units by clicking on the unit name and selecting the one you need.
- The quadrilateral area calculator displays the area, as well as the perimeter. The area is equal to 39,259 ft2, and the perimeter is 890 ft in our example. Now you know how much material you need to fence the parcel.
FAQs
How do I find the area of a quadrilateral given diagonals?
You cannot compute the area of a quadrilateral if you know only the length of its diagonals. You also need to know the angle between the diagonals. Then you can apply the formula:
area = diagonal1 × diagonal2 × sin(angle) / 2
What is Bretschneider's formula for quadrilaterals?
Bretschneider's formula is an expression allowing us to calculate the area of a general quadrilateral. It uses the four sides of the quadrilateral and two opposite angles. One can regard it as a generalization of Heron's formula for the area of a triangle given its sides.
How do I find the area of an irregular quadrilateral?
To determine the area:
-
Measure the four sides of the quadrilateral. Let's denote them by
a, b, c, d. -
Measure two opposite angles. Denote them
α, β. -
Compute the semiperimeter:
s = 0.5 × (a + b + c + d)
-
Plug the data into the formula:
area = √[(s - a) × (s - b) × (s - c) × (s - d) - a × b × c × d × cos²(0.5 × (α + β))]
What is the area of the kite with diagonals 2 and 5?
The answer is 5. Since the diagonals of a kite are perpendicular, the sine of the angle between them equals 1. Hence, the area formula reads area = diagonal1 × diagonal2 × 1 / 2. Plugging in the lengths of the diagonals, we obtain area = 2 × 5 × 1 / 2 = 5.