Irregular Polygon Area Calculator

Welcome to Omni's irregular polygon area calculator! With its help you can quickly determine the area of any irregular polygon. Our calculator uses the so-called shoelace formula.

Are you not sure what this formula is about? Do you want to learn how to calculate the area of irregular polygons by hand? Do you wonder what the shoelace formula has to do with shoelaces? Scroll down and find the answers to all your questions!

Recall that a polygon is a closed plane figure bounded by finitely many segments. Examples of polygons include triangles and rectangles. Examples of figures that are not polygons are ellipses and crescents. We say that a polygon is:

• simple (not self-intersecting) if its edges never cross; or

• self-intersecting (also called self-crossing or crossed) if some of its edges cross each other

  Self-intersecting polygons are sometimes called complex (in contrast to the term simple), but this can lead to confusion with the polygons in the complex plane (i.e., with two complex dimensions).

When it comes to computing areas, some polygons are better than others. Or at least easier to deal with 😉 For instance, we all know that it is easy to compute the area of a regular polygon, that is, of a polygon that is convex (all its interior angles are less than 180°), equilateral (all its sides have the same length), and equiangular (all its angles are equal). An example of a regular polygon is a square. You can discover more in the area of regular polygon calculator. Also, we have dedicated tools for some specific irregular polygons. Examples include:

• Parallelogram area calculator;
• Trapezoid area calculator;
• Rhombus area calculator; and
• Kite area calculator.

What to do if we have to determine the area of an irregular polygon for which there is no dedicated area of irregular polygon formula? Fortunately, there is a way! We will explain it to you in the next section.

The shoelace formula (a.k.a. Gauss's area formula) is a smart way of determining the area of a simple polygon (i.e., without self-intersections). All you need to know is the Cartesian coordinates of the vertices of the polygon.

💡 Tip. If you want to find the area of a self-intersecting polygon, you first have to divide it into two (or more) polygons that have no self-intersections.

Suppose that a simple polygon has vertices

(x₁, y₁), (x₂, y₂), ... , (x_n, y_n)

listed in clockwise or counterclockwise order. Then we can find the area of this polygon with the help of the following formula:

Area = 0.5 × |x₁y₂ - y₁x₂ + x₂y₃ - y₂x₃ + ... + x_ny₁ - y_nx₁|

where |x| is the modulus of x.

1. Enter the Cartesian coefficients of the polygon, both the x-coordinate and the y-coordinate. You can enter up to 30 vertices.

   • Make sure you're dealing with a simple polygon, i.e., one that has no self-intersections. If you're not, divide it into two (or more) simple polygons.

   • Make sure to enter the vertices in the counter-clockwise or clockwise order.

   • If your polygon has more than 30 vertices, divide it into two (or more) polygons and compute their areas separately, and then add all these areas to get the area of your original polygon.

2. Our calculator determines the area of your polygon and, as a bonus, its perimeter. The results will appear below the list of vertices.

3. If you want our irregular polygon area calculator to determine the results with higher precision, go to the advanced mode. By default, the calculator displays 4 sig figs.

So we have learned how to find the area of an irregular polygon with the help of the shoelace formula (or the shoelace theorem):

Area = 0.5 × |(x₁y₂ − y₁x₂) + (x₂y₃ − y₂x₃) + ... + (x_n-1y_n − y_n−1x_n) + (x_ny₁ − y_nx₁)|

But why, WHY is it called the shoelace formula? It's about polygons and calculations, not about shoes and laces, right? That's correct, but we will show you now that there is a reason behind this term. And, thanks to such a strange name, you hopefully have a better chance of remembering this formula!

So, let us list the coordinates of the vertices of our polygon in a column as follows:

x₁, y₁

x₂, y₂

x₃, y₃

...

x_n−1, y_n−1

x_n, y_n

x₁, y₁

As you can see, the first vertex appears again at the end of the list.

Now, to get the expression under the modulus at the right-hand side of the shoelace formula, we go from the top to the bottom of our column and mark the pairs of numbers to be multiplied. By doing so, we arrive at an image that resembles laced-up shoes — as in the picture below.

It is vital you remember that for each pair of rows:

• When we multiply the upper-left and bottom-right numbers, we take their product with the + sign.

• When we multiply the upper-right and bottom-left numbers, we take their product with the - sign.

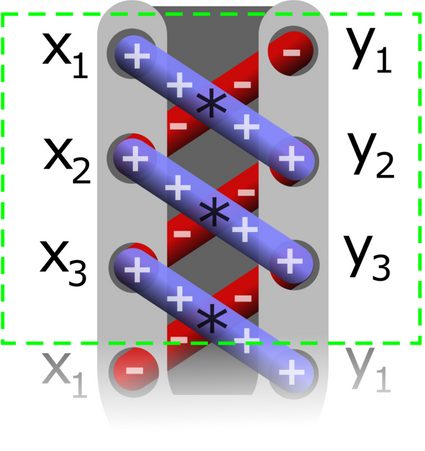
For those of you familiar with matrices, there is one more way to remember the shoelace formula. Namely, we can express the area of our polygon as 0.5 times the sum of the determinants of the following 2x2 matrices:

As an example, let's compute the area of the following Pacman-shaped polygon:

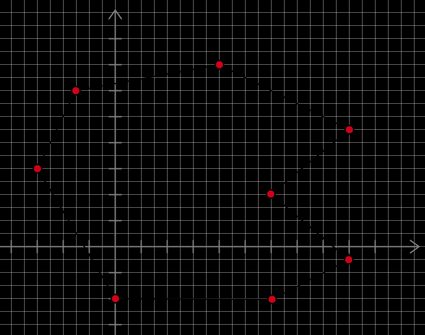
The coordinates of its vertices read:

(0, -2),
(6, -2),
(9, -0.5),
(6, 2),
(9, 4.5),
(4, 7),
(-1, 6),
(-3, 3).

Let's write them in a column, repeating the first vertex at the end of the column:

0, -2

6, -2

9, -0.5

6, 2

9, 4.5

4, 7

-1, 6

-3, 3

0, -2

We now go through this list and cross-multiply the numbers, remembering to apply the correct signs:

0 × (-2) - (-2) × 6 = 12

6 × (-0.5) - (-2) × 9 = 15

9 × 2 - (-0.5) × 6 = 21

6 × 4.5 - 2 × 9 = 9

9 × 7 - 4 × 4.5 = 45

4 × 6 - 7 × (-1) = 31

(-1) × 3 - 6 × (-3) = 15

(-3) × (-2) - 3 × 0 = 6

The sum of all these terms is 154. Halving this, we get the area of the Pacman:

Area = 0.5 × 154 = 77

A parallelogram is an irregular polygon because its interior angles are not equal.

The sides and angles of a regular polygon are always equal.

One way to find the area of an irregular polygon is to follow these steps:

1. Enclose the polygon in a rectangle.
2. Place evenly-spaced dots (with a known distance between them) inside this rectangle to divide it into equal parts.
3. Using these dots:
   • Find the area of the rectangle.
   • Find the area of the rectangle that is not covered by the shape.
4. Subtract these two areas from one another to obtain an estimate of the polygon's area.

The area is 20. We find this by following these steps:

1. List the coordinates, repeating the first one at the end.

2. Multiply each x coordinate by the y coordinate diagonally above it:
   5×6=30, 8×6=48, 4×1=4, 1×1=1

3. Multiply each x coordinate by the y coordinate diagonally below it:
   1×6=6, 5×1=5, 8×1=8, 4×6=24

4. Sum the pairwise differences between these two series' values:
   (30-6) + (48-5) + (4-8) + (1-24) = 40

5. Multiply the result by 0.5 to obtain the area:
   Area = 0.5 × 40 = 20

Yes, isosceles triangles are irregular polygons. To be a regular polygon, all sides and angles of a shape must be equal. An isosceles triangle has two equal sides and one unique side — the same goes for its angles. Therefore, an isosceles triangle is not regular.