Kite Area Calculator

If you are looking for the formula for kite area or perimeter, you're in the right place: the kite area calculator is here to help you. Whether you know the length of the diagonals or two unequal side lengths and the angle between, you can quickly calculate the area of a kite. For the kite perimeter, all you need to do is enter two kite sides. But if you are still wondering how to find the area of a kite, keep scrolling!

If it's not a kite area you are looking for, check our kiteboarding calculator, which can help you choose the proper kite size.

A kite is a quadrilateral with two pairs of equal-length sides adjacent to each other. A kite is a symmetric shape, and its diagonals are perpendicular. There are two basic kite area formulas, which you can use depending on which information you have:

1. If you know two diagonals, you can calculate the area of a kite as:

   area = (e × f) / 2 , where e and f are kite diagonals.

2. If you know two non-congruent side lengths and the size of the angle between those two sides, use the formula:

   area = a × b × sin(α), where α is the angle between sides a and b.

Did you notice that it's a doubled formula for the triangle area, knowing side-angle-side? Yes, that's right! A kite is a symmetric quadrilateral and can be treated as two congruent triangles that are mirror images of each other.

To calculate the kite perimeter, you need to know two unequal sides. Then, the formula is obvious:

perimeter = a + a + b + b = 2 × (a + b)

You can't calculate the perimeter knowing only the diagonals – we know that one is a perpendicular bisector of the other diagonal, but we don't know where is the intersection.

Let's imagine we want to make a simple, traditional kite. How much paper/foil do we need? And if we're going to make an edging from a ribbon, what length is required?

1. Think for a while and choose the formula which meets your needs. Assume we found two sticks in the forest; let's use them for our kite!

2. Enter the diagonals of the kite. The ones we have are 12 and 22 inches long.

3. Area of a kite appears below. It's 132 in².

Calculation of the kite perimeter is a bit tricky in that case. Let's have a look:

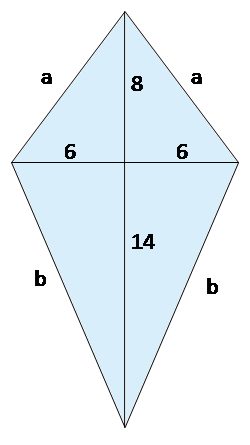
1. Assume you've chosen the final kite shape – you've decided where the diagonals intersect each other. For example, the shorter one will be split in the middle (6 in : 6 in) and the longer one in the 8:14 ratio, as shown in the picture.

2. Next, the easiest way is to use our right triangle calculator (this method works only for convex kites). Type 6 and 8 as a and b – the hypotenuse is one of our kite sides, here equal to 10 in. Refresh the calculator and enter 6 and 14 – the result is 15.23 in, and that's our other side.

3. Here you go! As we know both sides, we can calculate the perimeter. Type the a and b sides. The result for our case is 50.46 in. So buy a little bit more ribbon than that, for example, 55 inches, to make the edging.

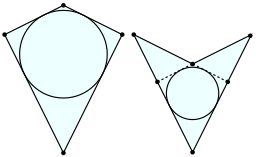
The kite can be convex – it's the typical shape we associate with the kite – or concave; such kites are sometimes called a dart or arrowheads. The area is calculated in the same way, but you need to remember that one diagonal is now "outside" the kite. The kite area calculator will work properly also for the concave kites.

The answer is almost always no. It's working the other way around – every rhombus is a kite. Only if all four sides of a kite have the same length, it must be a rhombus (see the rhombus area calculator) – or even a square, if all the angles are right.