Error Function Calculator

Welcome to the error function calculator! It helps you compute the values of the four function from the erf family:

• Error function itself;
• Complementary error function;
• Inverse error function; and
• Inverse complementary error function.

If you are not sure what the Gaussian error function actually is, don't worry! If you scroll down, you will find all the necessary definitions and plots, as well as a short explanation of why the error function matters. As a bonus, we will show you how to (approximately) calculate erf by hand! Finally, at the very bottom of the page, you can find the error function table.

The error function (often abbreviated to erf, also known as the Gaussian error function) is a special function that we encounter in applied mathematics and mathematical physics, e.g., in solutions to the heat equation.

For a real number x, the erf function is defined as

In the plot below, we see that erf is an odd sigmoid function.

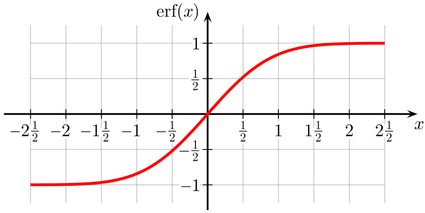
In statistics and probability theory, the error function has the following interpretation: for a random variable Z that follows the normal distribution with mean 0 and variance 0.5, the probability that Z falls in the interval [−x, x] is equal to erf(x), where we assume that x is non-negative. As a consequence, the error function is involved in many different calculations, in particular those you can encounter in the following Omni tools:

• p-value calculator;
• Confidence intervals calculator; and
• Critical values calculator.

Complementary error function

The complementary error function, most often denoted by erfc, is defined as one minus the error function. That is, we have

which we can also write as

In statistics, the complementary error function erfc(x), where we assume that x is non-negative, describes the probability that a random variable Z following the Gaussian normal distribution with mean 0 and variance 0.5 falls outside the interval [−x, x].

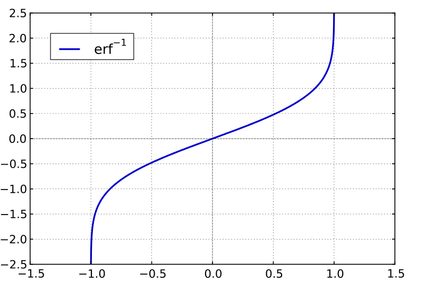
As we can see from the plot of the error function, if −1 < x < 1, then there exists a unique real number denoted erf^-1(x), such that:

In this way we obtain the inverse error function. Below you can see its plot:

Finally, there is the inverse complementary error function erfc^-1, which we define as

As the error function is a non-elementary function (as are the other three functions we defined above with the help of erf), it's not easy to find their values for a given argument x. Fortunately, Omni's erf calculator is here to help!

1. In the mode field, choose which of the four functions from the erf family you want to calculate.

2. Enter the value of the argument at which you want the function evaluated.

3. Our error function calculator returns the answer immediately. Enjoy!

What if one day you need to determine the Gaussian error function without a dedicated calculator at hand? Your situation isn't hopeless. There are several good ways of approximating erf. Let us mention two of them.

1. The error function has the following Taylor (Maclaurin) series:

It holds for all real arguments x. In practical applications, you need to compute a partial sum of this series, i.e., the sum of several initial terms. The more, the better the approximation.

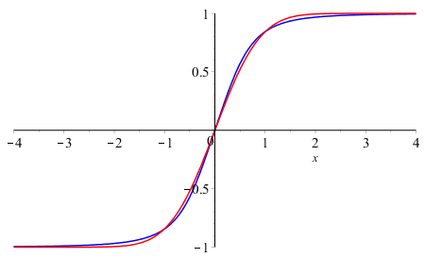
2. It turns out that a suitably transformed cyclometric (inverse trigonometric) function, arctan, can serve as a quite good approximation of the error function:

The plot below shows these two functions so that you can see how good the approximation is.

Since erf is a special function and cannot be easily calculated without a dedicated calculator, there's been a long tradition of tabulating its values. In case you ever need such a table, we give it below. It covers the arguments between 0 and 3. For negative arguments you need to utilize the fact that erf is an odd function, i.e., that erf(-x) = -erf(x).