p-value Calculator

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly. Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample. It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H₀ is true!

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means, so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H₀) is the probability of an event, calculated under the assumption that H₀ is true:

1. Left-tailed test: p-value = Pr(S ≤ x | H₀)

2. Right-tailed test: p-value = Pr(S ≥ x | H₀)

3. Two-tailed test:

   p-value = 2 × min{Pr(S ≤ x | H₀), Pr(S ≥ x | H₀)}

   (By min{a,b}, we denote the smaller number out of a and b.)

   If the distribution of the test statistic under H₀ is symmetric about 0, then:
   p-value = 2 × Pr(S ≥ |x| | H₀)

   or, equivalently:
   p-value = 2 × Pr(S ≤ -|x| | H₀)

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

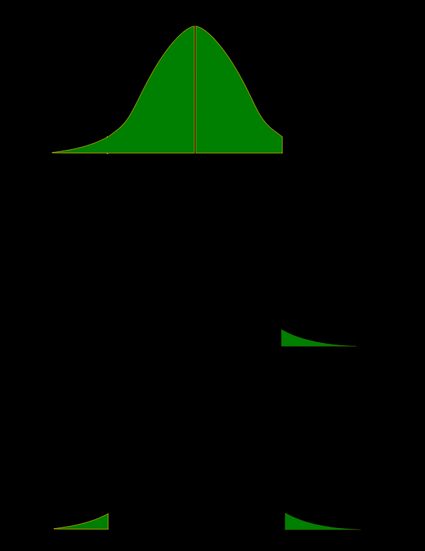
• Non-symmetric case: chi-squared distribution:

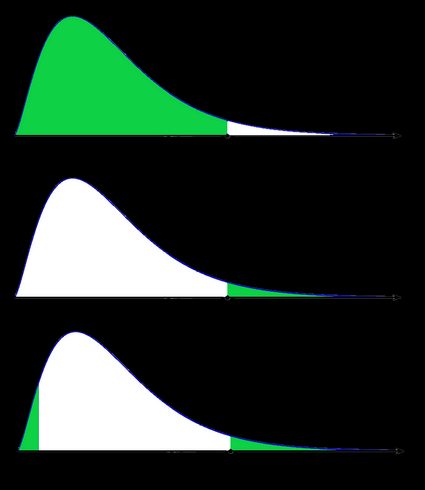
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true. Then, with the help of the cumulative distribution function (cdf) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

1. Left-tailed test:

   p-value = cdf(x).

2. Right-tailed test:

   p-value = 1 - cdf(x).

3. Two-tailed test:

   p-value = 2 × min{cdf(x) , 1 - cdf(x)}.

   If the distribution of the test statistic under H₀ is symmetric about 0, then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|), or, equivalently, as p-value = 2 - 2 × cdf(|x|).

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach. Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis, as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03. This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α, just compare your p-value with α:

• If p-value ≤ α, then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α, then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α. For instance, if the p-value was 0.03, we would reject the null hypothesis at a significance level of 0.05, but not at a level of 0.01. That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

1. Pick the alternative hypothesis: two-tailed, right-tailed, or left-tailed.

2. Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

3. If needed, specify the degrees of freedom of the test statistic's distribution.

4. Enter the value of test statistic computed for your data sample.

5. Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level.

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ, the p-value is given by the following formulae:

1. Left-tailed z-test:

   p-value = Φ(Z_score)

2. Right-tailed z-test:

   p-value = 1 - Φ(Z_score)

3. Two-tailed z-test:

   p-value = 2 × Φ(−|Z_score|)

   or

   p-value = 2 - 2 × Φ(|Z_score|)

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1). Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean, or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf_t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

1. Left-tailed t-test:

   p-value = cdf_t,d(t_score)

2. Right-tailed t-test:

   p-value = 1 - cdf_t,d(t_score)

3. Two-tailed t-test:

   p-value = 2 × cdf_t,d(−|t_score|)

   or

   p-value = 2 - 2 × cdf_t,d(|t_score|)

Use the t-score option if your test statistic follows the t-Student distribution. This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom. If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations, with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples.

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution.

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score? You can do it with the help of the following formulae, in which cdf_χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

1. Left-tailed χ²-test:

   p-value = cdf_χ²,d(χ²_score)

2. Right-tailed χ²-test:

   p-value = 1 - cdf_χ²,d(χ²_score)

   Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

3. Two-tailed χ²-test:

   p-value = 2 × min{cdf_χ²,d(χ²_score), 1 - cdf_χ²,d(χ²_score)}

   (By min{a,b}, we denote the smaller of the numbers a and b.)

The most popular tests which lead to a χ²-score are the following:

• Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test.

• Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test.

• Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test.

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution, also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom.

To see where those degrees of freedom come from, consider the independent random variables X and Y, which both follow the χ²-distributions with d₁ and d₂ degrees of freedom, respectively. In that case, the ratio (X/d₁)/(Y/d₂) follows the F-distribution, with (d₁, d₂)-degrees of freedom. For this reason, the two parameters d₁ and d₂ are also called the numerator and denominator degrees of freedom.

The p-value from F-score is given by the following formulae, where we let cdf_F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d₁, d₂)-degrees of freedom:

1. Left-tailed F-test:

   p-value = cdf_F,d1,d2(F_score)

2. Right-tailed F-test:

   p-value = 1 - cdf_F,d1,d2(F_score)

3. Two-tailed F-test:

   p-value = 2 × min{cdf_F,d1,d2(F_score), 1 - cdf_F,d1,d2(F_score)}

   (By min{a,b}, we denote the smaller of the numbers a and b.)

Below we list the most important tests that produce F-scores. All of them are right-tailed tests.

• A test for the equality of variances in two normally distributed populations. Its test statistic follows the F-distribution with (n - 1, m - 1)-degrees of freedom, where n and m are the respective sample sizes.

• ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k)-degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

• A test for overall significance of regression analysis. The test statistic has an F-distribution with (k - 1, n - k)-degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

  With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R², which indicates the strength of this relationship. You can do it by hand or use our coefficient of determination calculator.

• A test to compare two nested regression models. The test statistic follows the F-distribution with (k₂ - k₁, n - k₂)-degrees of freedom, where k₁ and k₂ are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

  You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.