Cotangent Calculator

Welcome to Omni's cotangent calculator, where we'll study the cot trig function and its properties. Arguably, among all the trigonometric functions, it is not the most famous or the most used. Nevertheless, you can still come across cot x (or cot(x)) in textbooks, so it might be useful to learn how to find the cotangent. Fortunately, you have Omni to provide just that, together with the cot definition, formula, and the cotangent graph.

So what is this cot exactly? Well, why don't we jump to the first section and find out?

Quite possibly (although we can never be sure), when ancient Greeks began studying triangles, they were not aware of what they started. For instance, when Pythagoras came up with his theorem, he probably didn't think to himself: "I bet it'll lead to some flimsy curves that all high school students will have to memorize someday." Still, that is precisely what happened.

Even if their attempts at looking into the future were faulty at best, they did get one thing right: right triangles are important. It turned out that not only do they have to satisfy the famous a² + b² = c² formula, but also their sides and inside angles are connected. After all, we can easily imagine that if one angle (not the right one, mind you) increases, then the opposite side must get larger as well. This concept, in essence, is the idea behind trigonometry.

Trigonometric functions describe the ratios between the lengths of a right triangle's sides. Below you can find them all, including the cot definition.

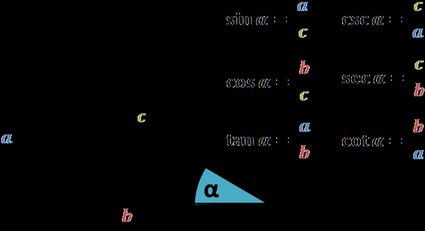
So what is the cotangent? According to the picture above, the cot formula is: divide the side next to the angle by the other one. What is more, the strength of that definition (and the other five, in fact) lies in the fact that, in some sense, the lengths of the triangle's sides do not matter. That is, if we scale the triangle to a larger or smaller size but keep the angle intact, the ratios (and with them, the cotangent function and the others) will not change.

With all their strengths, there is also a slight weakness to the cot definition we gave above: it only allows angles from 0 to 90 degrees (or from 0 to π/2 in radians). After all, it is a right triangle. Fortunately for us, there is a way to have all of the functions (including our beloved cot trig function) extended to any angle, even a negative one. The trick is to move the whole reasoning to the two-dimensional Euclidean space, i.e., the plane.

Let A = (x,y) be a point on the plane, and let α be the angle going counterclockwise from the positive half of the horizontal axis to the line segment connecting (0,0) and A. (Observe how we said that α goes from one line to the other and not that it is between them. Because of that, we often call α a directed angle.)

Needless to say, such an angle can be larger than 90 degrees. We can even have values larger than the full 360-degree angle. For that, we just consider 360 to be a full circle around the point (0,0), and from that value, we begin another lap. What is more, since we've directed α, we can now have negative angles as well by simply going the other way around, i.e., clockwise instead of counterclockwise.

So what is cot in this new language? In the trigonometric function definitions above, we substitute a for y, b for x, and c for √(x² + y²) (the distance from (0,0) to A that corresponds to the hypotenuse). This way, we get a new cotangent formula:

cot(α) = x / y.

But there are new questions to answer. For instance, what would cot 0 be? After all, for such an angle, the y coordinate is zero, and we can't divide by zero, can we?

Still, we got some answers so far. We've established the cot definition that we're all happy with (we are, aren't we?), so it's time for the next step: analyzing the cot function. And since we like pretty pictures, we'll start by drawing the cotangent graph.

You might have already seen the graph of the tangent function. Believe it or not, the similarity in the name is not coincidental. Who'd have thought, right? So if you recall the tangent function graph, you can play "spot the difference" with the cotangent graph below. (Note that this is the same picture that we use in our cotangent calculator.)

We can already read off a few important properties of the cot trig function from this relatively simple picture. To have it all neat in one place, we listed them below, one after the other.

• The cotangent function admits all real values. This means that for some angles, it will be tiny (say, -10,000,000 or -10⁷ if you prefer scientific notation), while for others, it'll be quite large.

• The cot in math language is odd. This means that the value at angle x is the opposite of that at -x. In other words, we have cot(x) = -cot(-x).

• The cotangent function is periodic with a 360-degree period. This characteristic means that the function's values repeat every 360 degrees. In mathematical notation, we can write this fact as cot(x) = cot(x + 360°).

• Similarly to the tangent (and, in fact, the secant and cosecant), the cotangent function doesn't always exist. For angles x of the form x = k·180° with k an integer, cot x is undefined. On the cotangent graph above, we see that the curve goes to plus/minus infinity at these points.

Let's take a moment and add a few more words to the last point above. The fact that the function is undefined in some places (for instance, cot 0 is undefined) results from the cot definition. After all, according to the above section and the cotangent formula we had there, the map is defined as a fraction. As we all know, we can't have zero in the denominator. That is precisely what happens with cot x in points x = k·180°. For example, for k = 0, we have the cot 0 that we've been so worried about.

Therefore, the cotangent function's domain consists of all points that are not of the form x = k·180° with k as an integer. If we wanted to please some of the big-headed mathematicians, we could write this fact as follows:

D(cot) = {x : x ≠ k·180°, k ∈ ℤ},

where D(cot) denotes the domain of cot in math notation.

Alright, we're moving swiftly! Admittedly, we're not being paid by the hour here, but it's still satisfying to see how much we've managed to cover so far. And it's not the end just yet! We've got to know how to find the cotangent using right triangles and Euclidean coordinates. But is there some other way? Well, the title of the next section suggests what the answer is, doesn't it?

Once you get familiar with trigonometry on the level of functions, you move on to analyzing the correspondences between them. In other words, you search for identities that they must satisfy or ways of expressing one with the others. To encourage you to delve into the topic, let's mention two famous formulas that we often use when dealing with triangles: the law of sines and the law of cosines.

However, let's look closer at the cot trig function which is our focus point here.

Firstly, we've already mentioned that tan x and cot x are connected not only by the similarity in the names. Recall from the first section that the tangent, and cotangent formulas used the same sides of the triangle: the two legs. The only difference is that the cot definition flips them as compared to tan. Therefore, we arrive at our first alternative cot formula:

cot(x) = (tan(x))⁻¹.

Or, if you prefer fractions,

cot(x) = 1 / tan(x).

Note, however, that this does not mean that it's the inverse function to the tangent. That would be the arctan map, which takes the value that the tan function admits and returns the angle which corresponds to it. Here, we can only say that cot x is the inverse (not the inverse function, mind you!) of tan x.

But we're not done just yet! There is one more useful cot formula that we'd like to mention. It connects the cotangent function to two other trigonometric maps: the sine and the cosine.

We have:

cot(x) = cos(x) / sin(x).

In fact, you might have seen a similar but reversed identity for the tangent. If so, in light of the previous cotangent formula, this one should come as no surprise.

Together with the cot definition from the first section, we now have four different answers to the "What is the cotangent?" question. It seems more than enough to leave the theory for a bit and move on to an example that actually has numbers in it.

Shall we?

Suppose that after a brief introduction to the fascinating world of trigonometry, your teacher decided that it's time to check how much of what they said stayed in your brains. They announced a test on the definitions and formulas for the functions coming later this week.

The amount of material to learn is not that big, and there are still quite a few days left, but being the good student that you are, you choose to start preparing today. You tidy up your desk and for practice, decide to calculate the values of all the trigonometric functions on the following angles: 30°, 45°, 60°, and 75°. In this article, we're most interested in how to find the cotangent of these angles.

First of all, let's see how easy the task is with Omni's cot calculator. There, we only have one variable field to fill: the angle. We input the above numbers one by one, and the cotangent calculator spits out the answer underneath. Note that although the cotangent calculator strives for precision, you might wish to reduce the number of significant figures if you're going to use the values in some further calculations.

Also, observe how for 30° and 60°, it gives you precise values before rounding them up, i.e., in the form of a fraction with square roots. We will speak more about why it is so in a second.

Now, it's time to leave the cotangent calculator for a while and use what we've learned in this article. In other words, we'll calculate the values ourselves using the cotangent definition from the first section. (Of course, if you prefer, you may use any of the other three cot formulas.)

For each angle, we'll begin with a drawing of a right triangle with the corresponding angle. We start with the first one: 30°.

Observe that this is quite a special triangle in which we know the relations between the sides, i.e., we can be sure that if the shorter leg is of length x, then the hypotenuse will be 2x. This is because our shape is, in fact, half of an equilateral triangle. As such, we have the other acute angle equal to 60°, so we can use the same picture for that case.

Recall that cot in math is the ratio of the leg next to the angle to the other one. So what is the cotangent in this case? We have:

cot(30°) = x√3 / x = √3,

and:

cot(60°) = x / x√3 = 1 / √3 = √3 / 3.

Next, we move on to the 45° angle.

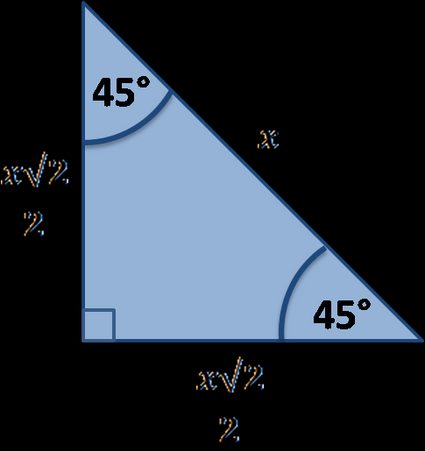
Again, we are fortunate enough to know the relations between the triangle's sides. This time, it is because the shape is, in fact, half of a square.

We use the cotangent definition to get:

cot(45°) = x / x = 1.

So we're left with the last angle. What is the cotangent of 75°?

Well, as it occurs, the answer is not so simple. We have no special triangle to use here. We could, for instance, recall the previous section and find the answer by calculating tan(75°) first. For that, however, we would have to use, for instance, the half-angle formulas, which would, in turn, require us to find cos(150°). This problem, eventually, is not that difficult since 150° = 180° - 30°, and both 30° and 180° are fairly simple angles.

The lesson here is that, in general, calculating trigonometric functions is no walk in the park. In fact, we usually use external tools for that, such as Omni's cotangent calculator.

Nevertheless, these few simple calculations were surely a good preparation for the upcoming test. Once you get your final grade in mathematics, look back at all the memories you've shared with Omni Calculator that helped you along the way, and give us a satisfied nod of the head. The poor content developers are hungry for those. 😀