Width of a Rectangle Calculator

Q: How do I calculate the width of a rectangle?

Depending on what information you have available , there are many ways to calculate the width of a rectangle. If you have the area A and length h , its width w is w = A/h . If you have the perimeter P and length h , its width is w = P/2−h . If you have the diagonal d and length h , it's width can be found with w = √(d²−h²) . If the rectangle's length is not known, you'd need to do some algebra with the quadratic equation to solve for the width.

Q: What is the width of a rectangle with length 4 m and area 20 m?

Using the formula for a rectangle's area , A = h × w , we can follow these steps: Rewrite the area formula to make the width w the subject of the equation: w = A/h . Plug in the values: w = 20/4 . Do the math and find that w = 5 m .

The width of a rectangle calculator can take two dimensions of your rectangle (height, area, diagonal, or perimeter) and work out the width of your rectangle. We'll also show you some formulas for the width of a rectangle, that are based on what information you have available. So don't be a square and read on!

How to use the width of a rectangle calculator?

Using the width of a rectangle calculator is easy, with only two steps. Here's how.

Enter the dimensions that you know of the rectangle.
Find your rectangle width in the bottom box.
The calculator is omni-directional — if you want to work backwards instead, you can change the rectangle's width and see how its other dimensions react.
And that's it! Now you know how to calculate the width of a rectangle!

How do I calculate the width of a rectangle?

Depending on what information you have available, there are many ways to calculate the width of a rectangle.

If you have the area A and length h, its width w is w = A/h.
If you have the perimeter P and length h, its width is w = P/2−h.
If you have the diagonal d and length h, it's width can be found with w = √(d²−h²).
If the rectangle's length is not known, you'd need to do some algebra with the quadratic equation to solve for the width.

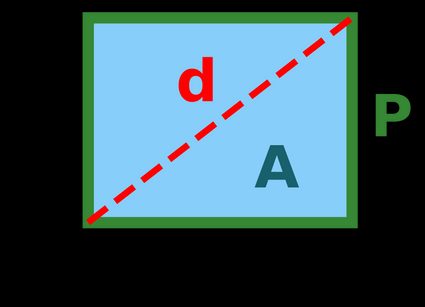
That's a lot of different formulas for the width of a rectangle! It's because there are multiple equations that govern the dimensions of a rectangle. Here they are:

\begin{split} A &= \textcolor{red}{w} \times h \\ P &= (\textcolor{red}{w}+h)\times 2 \\ d &= \sqrt{\textcolor{red}{w}^2 + h^2} \end{split}

where:

$w$ is the rectangle's width;
$h$ is the rectangle's length;
$A$ is the rectangle's area;
$P$ is the rectangle's perimeter; and
$d$ is the length of the rectangle's diagonal (as described by the Pythagorean theorem).

Here's a neat visual:

A rectangle with its length, width, diagonal, perimeter, and area labelled. — A rectangle with its length $h$ , width $w$ , diagonal $d$ , perimeter $P$ , and area $A$ labelled.

Related calculators

If the width of a rectangle calculator isn't quite what you want, try out our other rectangular calculators:

FAQs

What is the width of a rectangle?

A rectangle has four sides, but because the sides are paired, there are only two unique dimensions. Conventionally, the width is the shortest of these two dimensions, but when the rectangle is presented as lying on its side, the horizontal side is usually called the width.

What is the width of a rectangle with length 4 m and area 20 m?

Using the formula for a rectangle's area, A = h × w, we can follow these steps:

Rewrite the area formula to make the width w the subject of the equation: w = A/h.
Plug in the values: w = 20/4.
Do the math and find that w = 5 m.