Diagonal of a Rectangle Calculator

Our diagonal of a rectangle calculator is an extensive tool that quickly finds the diagonal and other parameters of a rectangle. Have you met a specific rectangle problem and you don't know how to find the diagonal of a rectangle? Try entering a couple of parameters in the fields beside the text or keep reading to find out what are the possible diagonal of a rectangle formulas.

You can see a typical rectangle in the figure below. We have marked five basic quantities that describe a specific rectangle. You can use them to derive the diagonal of a rectangle formula. These are:

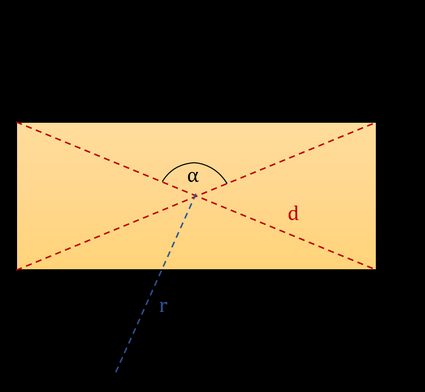
• l — Length;
• w — Width;
• α — The angle between diagonals;
• r — Circumcircle radius;
• d — Diagonal;

and two other parameters which are not shown in the picture:

• A – Area; and
• P – Perimeter.

The term rectangle comes from the Latin rectangulus, which is a combination of two words: rectus (right, proper) and angulus (angle). This name derives from the fact that a rectangle is a quadrilateral with four right angles (4 × 90° = 360°). Its opposite sides are parallel and of equal length, and its two diagonals intersect each other in the middle and are of equal lengths, too.

A square is a special case of a rectangle. Its definition is that it has all four sides of equal length; alternatively, the angle between two diagonals is right. Try our calculators dedicated to squares, e.g., the square calculator. They can quickly estimate the perimeter, area, and diagonal of every square you want, just from the length of its side.

The center of a rectangle is equidistant from its vertices; therefore, you can always circumscribe a circle on it. On the other hand, you can inscribe a circle into a rectangle only if it is a square.

To determine the diagonal of a rectangle, you need to:

1. Write down the sides of the rectangle, which we denote by w and l.
2. Square these two values. That is, compute l² and w².
3. Add together the two squared values from Step 2.
4. Take the square root of the result.
5. That's it! You've just found the length of the diagonal of your rectangle.

Why does this procedure work?

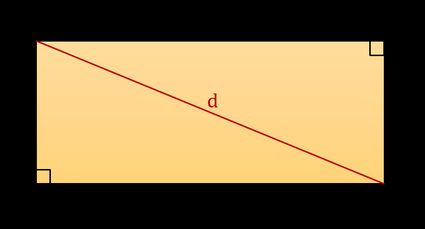
To derive the diagonal of a rectangle formula used above, divide a rectangle into two congruent right triangles, i.e., triangles with one angle of 90°. Each triangle will have sides of length l and w and a hypotenuse of length d. You can use the hypotenuse formula, e.g., from the Pythagorean theorem calculator, to estimate the diagonal of a rectangle, which can be expressed with the following formula:

d² = l² + w²

and now you should know how to find the diagonal of a rectangle explicit formula - just take a square root:

d = √(l² + w²)

Our diagonal of a rectangle calculator allows you to use almost any units you want. Check out our length converter or area converter to find out how to switch between different units (SI and imperial).

Sometimes, you won't have given the length of two adjacent sides of a rectangle. How do you find the diagonal of a rectangle in that situation? The answer is provided using our diagonal of a rectangle calculator. First, let's write down three basic equations for the area, perimeter, and circumcircle radius:

1. Area of a rectangle: A = w × l.
2. Perimeter of a rectangle P = 2 × w + 2 × l.
3. Circumcircle radius of a rectangle r = d/2.

With the above equations, we can now derive various diagonal of a rectangle formulas that are used by this diagonal of a rectangle calculator:

1. Given length and width:

   d = √(l² + w²)

2. Given length/width and area:

   d = √(A²/l² + l²) or d = √(A²/w² + w²)

3. Given length/width and perimeter:

   d = √(2l² − P × l + P²/4)) or d = √(2w² − P × w + P²/4)

4. Given length/width and angle:

   d = w / sin(α/2) or d = l / cos(α/2)

5. Given area and perimeter:

   d = ½√(P² − 8 × A)

6. Given area and angle:

   d = √(2 × A / sin(α))

7. Given perimeter and angle:

   d = P / (2 × sin(α/2) + 2 × cos(α/2))

8. Given circumcircle radius:

   d = 2 × r

Note: The angle α between diagonals is opposite the side with length l, as shown in the first figure. Also, remember that the diagonal of a rectangle calculator assumes that the length is longer than the width!

Did you know that there is a special rectangle called the golden rectangle? If not, head on to our golden rectangle calculator to learn how you can construct golden rectangles!