Length Of A Rectangle Calculator

Q: How do I calculate the length of a rectangle?

Depending on what information you have available , there are many ways to calculate the length of a rectangle. If you have the area A and width w , its length h is determined as h = A/w . If you have the perimeter P and width w , its length can be found with h = P/2−w . If you have the diagonal d and width w , it's length is h = √(d²−w²) . If the rectangle's width is not known, you'd need to simultaneously solve the system of equations above to get the length h .

Q: What is the length of a rectangle with diagonal 5 m and width 3 m?

4 m . Because the connected sides of a rectangle are perpendicular , we can use the Pythagoras theorem to work this one out. Rearrange the Pythagoras theorem to make the rectangle's length h the subject: h = √(d²−w²) . Plug in your values: h = √(5²−3²) = √(25-9) = √16 = 4 .

Creators

Rijk de Wet

Website

A self-described nerd, Rijk is passionate about making a positive difference in the lives of Omni’s users. He’s an avid programmer, musician, and board game player, and both his calculators and side-projects reflect his hobbies. He believes that any problem can be solved with the right set of equations and a few lines of code. See full profile

Check our editorial policy

Reviewers

Aleksandra Zając, MD

Aleksandra Zając

Website

Aleksandra (Ola) Zając, MD, is a medical doctor with a passion for lifestyle medicine. She wants to never stop learning while sharing what she already knows as a health educator and prophylaxis popularizer. She mainly concentrates on how human lifestyle impacts their health and disease. After hours, she likes weightlifting, foreign affairs podcasts, learning Korean, and dogs (with a special affection for her own pup Zoja). See full profile

Check our editorial policy

New

Welcome to the length of a rectangle calculator, where we'll explain the formula(s) for the length of a rectangle and how to find the length of a rectangle.

How to use the length of a rectangle calculator?

Using the length of a rectangle calculator is easy — there's only two steps!

Enter the dimensions that you know of the rectangle.
Find your rectangle length in the bottom box.
The length of a rectangle calculator works both ways — try changing the rectangle's length and see how its other dimensions are affected.
Not enough to just know how to use the length of a rectangle calculator? Read on to learn how to calculate the length of a rectangle.

How do I calculate the length of a rectangle?

Depending on what information you have available, there are many ways to calculate the length of a rectangle.

If you have the area A and width w, its length h is determined as h = A/w.
If you have the perimeter P and width w, its length can be found with h = P/2−w.
If you have the diagonal d and width w, it's length is h = √(d²−w²).
If the rectangle's width is not known, you'd need to simultaneously solve the system of equations above to get the length h.

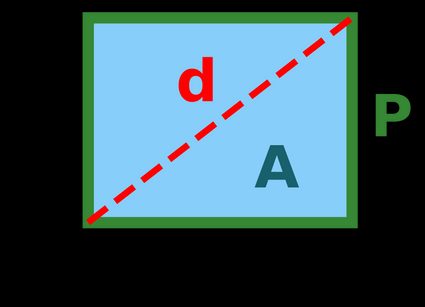
That's a lot of different formulas for the length of a rectangle! These are all derived from the many formulas that govern a rectangle's dimensions. Those formulas are:

\begin{split} A &= w \times \textcolor{red}h \\ P &= 2(w+\textcolor{red}h) \\ d &= \sqrt{w^2 + \textcolor{red}h^2} \end{split}

where:

$w$ is the rectangle's width;
$h$ is the rectangle's length;
$A$ is the rectangle's area;
$P$ is the rectangle's perimeter; and
$d$ is the length of the rectangle's diagonal, as described by the Pythagorean theorem.

Here's a neat visual:

A rectangle with its length, width, diagonal, perimeter, and area labelled. — A rectangle with its length $h$ , width $w$ , diagonal $d$ , perimeter $P$ , and area $A$ labelled.

FAQs

What is the length of a rectangle?

A rectangle has four sides. Its sides are paired, so really there are only two unique dimensions. Conventionally, the rectangle's length is the longest of these two measurements, but when the rectangle is shown to be standing on the floor, the vertical side is usually called the length.

What is the length of a rectangle with diagonal 5 m and width 3 m?

4 m. Because the connected sides of a rectangle are perpendicular, we can use the Pythagoras theorem to work this one out.

Rearrange the Pythagoras theorem to make the rectangle's length h the subject: h = √(d²−w²).
Plug in your values: h = √(5²−3²) = √(25-9) = √16 = 4.

How to use the length of a rectangle calculator?

How do I calculate the length of a rectangle?

Related calculators

What is the length of a rectangle?

What is the length of a rectangle with diagonal 5 m and width 3 m?