Perimeter of a Rectangle Calculator

Use our perimeter of a rectangle calculator if you need to estimate quickly what the perimeter of a specific rectangle is. Try to enter some values, or read on to learn more about rectangles. In the following text, we explain in detail how to find the perimeter of a rectangle with 10 different perimeter of a rectangle formulas.

The rectangle is a quadrilateral with four right angles (4 × 90° = 360°). Its name is derived from the Latin word rectangulus, which means right (rectus) angle (angulus). The opposite sides of the rectangle are parallel to each other and of equal length. A rectangle has two diagonals that intersect in the middle of the rectangle and are of equal lengths. In the picture below, you can see a typical rectangle with marked parameters:

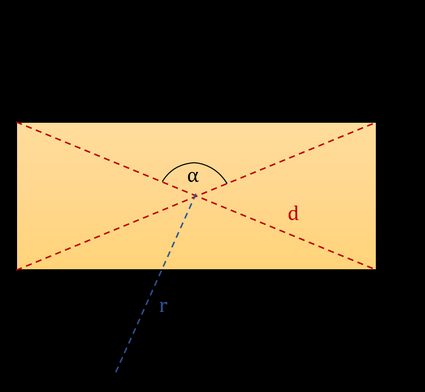
• $l$ — Length;
• $w$ — Width;
• $\alpha$ — Angle between diagonals;
• $r$ — Circumcircle radius; and
• $d$ — Diagonal.

There are two other characteristic quantities that are not shown in the picture:

• $A$ — Area; and
• $P$ — Perimeter.

You can always circumscribe a circle on the rectangle because its center is equidistant from all of its four vertices. Moreover, the center of this circle lies exactly at the intersection of two diagonals. However, you can't inscribe a circle into every rectangle. In fact, you can do it only with a square, which is a special case of a rectangle. A Square is a quadrilateral with four right angles and all four sides of equal lengths. Check out our perimeter of a square calculator or the diagonal of a square calculator if you need to solve specific problems with squares!

A perimeter is a path that surrounds any two-dimensional shape. You can think of it as a fence that is required to surround a yard or a garden. A circle is a special figure because a circle's perimeter is usually called the circumference.

So, how to find the perimeter of a rectangle? You need to sum up the lengths of every side:

$P = l + w + l + w$

$P = 2 l + 2 w$

$P = 2 (l + w)$

With this perimeter of a rectangle calculator, you can make calculations in almost any unit you want. To learn more about length units, check out our length converter!

To calculate the perimeter in the above equations, we have used two sides of a rectangle. However, in some mathematical problems, there are different quantities given. How to find the perimeter of a rectangle in these situations? Most of these problems can be solved with the perimeter of a rectangle calculator. Before we write down appropriate formulas, there are three basic equations for the area, diagonal, and circumcircle radius of a rectangle that you should remember:

1. Area of a rectangle: $A = w l$;
2. Diagonal of a rectangle $d = \sqrt{l^2 + w^2}$; and
3. Circumcircle radius of a rectangle $r = d/2$.

With the above equations, we can now derive various perimeter of rectangle formulas that are used by the calculator on this site:

1. Given length and width:

2. Given length/width and diagonal:

3. Given length/width and area:

4. Given length/width and angle:

5. Given length/width and circumcircle radius:

6. Given diagonal and area:

7. Given diagonal and angle:

8. Given area and angle:

9. Given area and circumcircle radius:

10. Given angle and circumcircle radius:

Note: The angle $\alpha$ between diagonals is in the front of the length like in the first figure. Also, remember that the perimeter of a rectangle calculator assumes that the length is longer than the width!

Have you ever heard about the golden rectangle? It is a special rectangle, the side lengths of which are in the golden ratio. Check out our golden rectangle calculator to learn more about constructing golden rectangles! If you want to learn about the ratio alone, then our golden ratio calculator is the right place to start.