Triangulation Calculator

Omni's triangulation calculator will find the coordinates of an unknown point based on two known locations and measuring the bearing either to or from those locations.

You can either:

• Calculate your position by observing two landmarks with known coordinates.
• Calculate the position of an unknown landmark by observing it from two known locations.

If you don't know what triangulation is or the formula for triangulation, worry not! Continue reading this article to know the definition of triangulation and the difference between triangulation and trilateration in surveying. You will also learn how to calculate coordinates using the triangulation calculator.

Triangulation, when related to geometry or surveying, is a method of determining the location of an unknown point by forming a triangle or triangles to it from known points.

There are two general types of triangulation:

• Intersection — You triangulate an unknown landmark by making multiple observations at different locations; and

• Resection — You determine your own position by observing multiple known landmarks from a single location.

To determine the triangulation formula for finding the location of a landmark, let us consider figure 1.

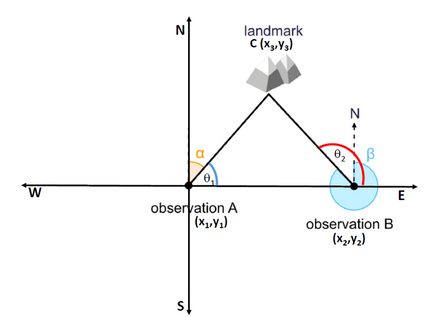
Let $A(x_1, y_1)$ and $B(x_2, y_2)$ be the two observation points with bearings towards the landmark as $\alpha$ and $\beta$, respectively. If $C(x_3, y_3)$ is the location of the landmark, the points $A$, $B$, and $C$ form the vertices of a triangle, where:

$\angle CAB = \theta_1$

and

$\angle CBE = \theta_2$.

Using coordinate geometry, we can write the formula for the slope of line AC as:

Similarly, for line BC, we can write:

To dive into the details of determining the slope in the Cartesian coordinate system, visit our slope calculator.

Solving equations (1) and (2) for $x_3$ and $y_3$, we get:

and

We can also determine the triangulation formula to locate our position with respect to two or more landmark points, as shown in figure 2.

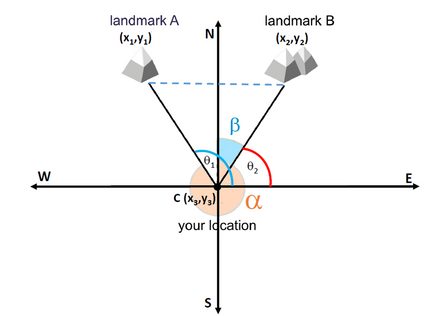
Let $A(x_1, y_1)$ and $B(x_2, y_2)$ be the two landmark points with bearings as $\alpha$ and $\beta$, respectively. If $C(x_3, y_3)$ is our location, the points $A$, $B$, and $C$ form the vertices of a triangle, where the angles are:

$\angle ACE = \theta_1$

and

$\angle BCE = \theta_2$.

We can write the formula for the slope of line AC as:

Similarly, for line BC, we can write:

Solving equations (3) and (4) for $x_3$ and $y_3$, we get:

and

Let us see how to use the triangulation calculator to determine the location of a landmark. We will consider A as the reference point for our measurement. Let the coordinates of points $A(x_1, y_1)$ and $B(x_2, y_2)$ be (0, 0) and (5, 0), respectively. The measured azimuth or bearings at point A and B be $\alpha = 30\degree$ and $\beta = 330\degree$.

1. Using the drop-down menu, select landmark location.

2. Enter the x, y coordinates, and the bearings ( $\alpha = 30\degree$ and $\beta = 330\degree$) of observation points $A(0, 0)$ and $B(5, 0)$ in the respective fields.

3. The coordinate triangulation calculator will display the coordinates of the landmark, i.e., (2.5, 4.33).

4. You can use our azimuth calculator to determine the azimuth if you know the latitudes and longitudes of the points.

Both triangulation and trilateration are methods of surveying based on trigonometry. However, while triangulation relies only on angle measurements to locate the unknown point, trilateration uses distance measurements.

Fun fact: While triangulation has an important history in surveying and navigation, GPS uses trilateration to determine your location, not triangulation (the satellites only measure distances)!

In land surveying, triangulation is the method of measuring the angles of a network of triangles. This information is then used to determine distances and relative positions of locations spread over the survey area using trigonometry.

The principle of the triangulation method is that if the coordinates of two vertices of a triangle (or the length of one of its sides) and its angles are known, we can calculate the coordinates of the third side (or the length of the remaining sides).

The main differences between triangulation and trilateration are:

• Triangulation relies on the measurement of angles. Trilateration relies on the measurement of sides.
• The measuring stations should be mutually visible for the triangulation method. In trilateration, the distances can be measured without the intervisibility of the stations.

Some common applications of the triangulation method are:

• In large-scale land surveying to determine the accurate position of locations.
• In civil engineering projects to accurately locate center line of long bridges and tunnels, etc.
• Land and sea navigation.