Distance Between Two Points Calculator

Our distance between two points calculator can quickly find the distance between any two points confined to a two-dimensional plane.

Within this short text, we will cover:

• How to find the distance between two points;
• How to use the distance between two points formula; and
• What is the shortest distance between two points.

Let's start!

Prefer watching rather than reading? Learn all you need in 90 seconds with this video we made for you:

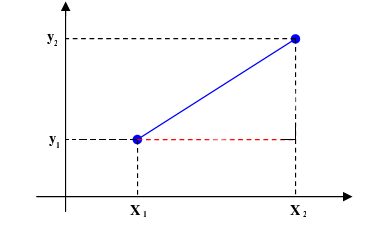
In its simplest definition, the distance between two points in a 2D plane is the length of the line segment connecting them.

For example, if we put into a graph the points $(0, 4)$ and $(4, 4)$, draw a line between them, and measure this line segment's length, we would get $4$ as a result.

This definition is derived from the Euclidean distance definition, and we can also define 1D, 3D, 4D, and any finite dimension Euclidean distance.

Of course, plotting and measuring lines anytime we want to find the distance between two points is not practical. That's where the distance between two points formula comes in.

We can obtain the mathematical distance definition from the Euclidean distance formula for a two-dimensional plane:

where:

• $x_{1}$ and $y_{1}$ are the coordinates of any of the two points;
• $x_{2}$ and $y_{2}$ are the coordinates of the other point; and
• $d$ is the distance between them.

To find the distance between two points, simply follow these steps:

1. Find the XY coordinates of the first point (x₁, y₁). It doesn't matter which point we choose as long as we don't mix coordinates between them.

2. Find the XY coordinates of the other point (x₂, y₂).

3. Replace these values in the distance between two points formula:

   √[(x₂ - x₁)² + (y₂ - y₁)²].

If you enjoyed this distance between two points calculator and want to learn more about other distance definitions, check any of our other distance calculation tools:

• Distance;
• 2D distance;
• Length of a line segment;
• Coordinate distance; and
• Euclidean distance.