Coordinate Distance Calculator
Table of contents
What is the distance formula for cartesian coordinates?How to use the coordinate distance calculatorLet's keep finding distances!FAQsUse the coordinate distance calculator to find the distance between two coordinates in a two-dimensional or three-dimensional space. By simply entering the XY or XYZ coordinates of the points, this tool will instantly compute the distance between them!
Along with this tool, we've created a brief text where you'll find:
- What the distance formula is for cartesian coordinates;
- How to use this formula for determining the distance between coordinates in the 2D or 3D spaces; and
- The distance formula for polar coordinates.
Enjoy! 😄
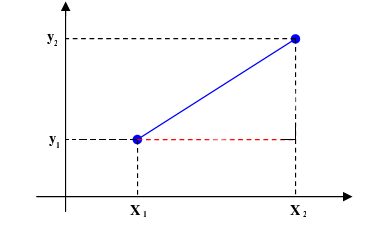
What is the distance formula for cartesian coordinates?
The general distance formula in cartesian coordinates is:
d = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
where:
- d — Distance between two coordinates;
- x₁, y₁ and z₁ — 3D coordinates of any of the points; and
- x₂, y₂ and z₂— 3D coordinates of the other point.
This formula, which derives from the Pythagorean theorem, is also known as the Euclidian distance formula for three-dimensional space.
Although this formula includes the z coordinate, you may use it for both 2D and 3D spaces. By setting the z coordinates to zero, you can get a particular version for the distance between two points in a 2D space:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Here d is the distance between two points in the two-dimensional space.
How to use the coordinate distance calculator
The coordinate distance calculator makes it simple to find the distance between two points given its cartesian coordinates. Let us see how to use this tool:
-
From the Dimensions field, choose between
2Dor3D, according to the dimensional space in which your points are defined. -
In the First point section of the calculator, enter the coordinates of one of the points.
-
Similarly, in the Second point section, input the coordinates' values of the other point.
-
Once you've entered these values, the calculator will display the distance between the points (
Distance) in the Result section.
🙋 Did you know that a 2D coordinate can be expressed as a 3D point that has a z coordinate equal to zero (x, y, 0)? This means you could as well use the 3D version of this coordinate distance calculator to find distances between 2D points by simply setting the z coordinates to zero.
Let's keep finding distances!
Now that you've mastered how to calculate the distance between two coordinates, you might want to take a look at some other related tools:
What is the 3D distance formula?
The 3D distance formula is:
d = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
where:
- d — Distance between the two coordinates;
- x₁, y₁ and z₁ — 3D coordinates of point one; and
- x₂, y₂ and z₂— 3D coordinates of point two.
How do I calculate the distance between the two coordinates?
To find the distance between two three-dimensional coordinates (-1, 0, 2) and (3, 5, 4):
-
Use the distance formula for 3D coordinates:
d = √[(x₂ - x₁)² + (y₂ - y₁)²+ (z₂ - z₁)²]
-
The variable's values from that equation are:
(x₁, y₁, z₁) = (-1, 0, 2)
(x₂, y₂, z₂) = (3, 5, 4) -
Substitute and perform the corresponding calculations:
d = √[(3 - -1)² + (5 - 0)² + (4 - 2)²]
d = √[(4)² + (5)² + (2)²]
d = √45 -
Calculate the square root to get the distance:
d = 6.70825
Can I calculate the distance between polar coordinates?
Yes. By employing the distance formula for polar coordinates d = √[r₁² + r₂² - 2r₁r₂cos(θ₁ - θ₂)], you can determine the distance between two polar coordinates in a two-dimensional or three-dimensional space.
What is the distance formula in polar coordinates?
The distance formula for polar coordinates is:
d = √[r₁² + r₂² - 2r₁r₂cos(θ₁ - θ₂)]
where:
- d — Distance between the two points;
- r₁ and θ₁ — Polar coordinates of point one; and
- r₂ and θ₂— Polar coordinates of point two.
