Length of a Line Segment Calculator

With the length of a line segment calculator, you can instantly calculate the length of a line segment from its endpoints.

If you're not sure of what a line segment is or how to calculate the length of a segment, then you might like to read the text below. In it, you'll find:

• What is a line segment?;
• The formula for the length of a line segment; and
• How to find the length of a segment with its endpoints.

If you glance around, you'll see that we are surrounded by different geometric figures. Perhaps you have a table, a ruler, a pencil, or a piece of paper nearby, all of which can be thought of as geometric figures.

If we look again at the ruler (or imagine one), we can think of it as a rectangle. In geometry, the sides of this rectangle or edges of the ruler are known as line segments. A line segment is one of the basic geometric figures, and it is the main component of all other figures in 2D and 3D.

With these ideas in mind, let's have a look at how the books define a line segment:

"A line segment is a section of a line that has two endpoints, A and B, and a fixed length. Being different from a line, which does not have a beginning or an end. The line segment between points A and B is denoted with a top bar symbol as the segment $\overline{AB}$."

Returning to the ruler, we could name the beginning of the numbered side as point A and the end as point B. According to the definition, this actually corresponds to a line segment with a beginning and an end (endpoints A and B) and a fixed length (ruler's length).

But what if the line segment we want to calculate the length of isn't the edge of a ruler? Great question! Another way to determine the length of a line segment is by knowing the position (coordinates) of its endpoints A and B.

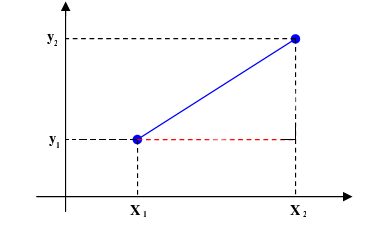
This implies that a line segment can be drawn in a coordinate plane XY. This coordinate plane representation of a line segment is very useful for algebraically studying the characteristics of geometric figures, as is the case of the length of a line segment.

In the sections below, we go into further detail on how to calculate the length of a segment given the coordinates of its endpoints.

The formula for the length of a line segment is given by the distance formula, an expression derived from the Pythagorean theorem:

d = √[(x₂ - x₁)² + (y₂ - y₁)²]

where:

• d — Length of the line segment;
• x₁ and y₁ — Coordinates of any of the endpoints of the line segment; and
• x₂ and y₂ — Coordinates of the other endpoint.

To find the length of a line segment with endpoints:

1. Use the distance formula:
   d = √[(x₂ - x₁)² + (y₂ - y₁)²]

2. Replace the values for the coordinates of the endpoints, (x₁, y₁) and (x₂, y₂).

3. Perform the calculations to get the value of the length of the line segment.

With this length of a line segment calculator, you'll be able to instantly find the length of a segment with its endpoints. To use this tool:

1. In the First point section of the calculator, enter the coordinates of one of the endpoints of the segment, x₁ and y₁.

2. Similarly, in the Second point section, input the coordinates' values of the other endpoint, x₂ and y₂.

3. Finally, the calculator will display the length of the segment (Length) in the Result section.

4. That's it! 😄

Did you find the length of a line segment calculator useful? If you did, you might like to visit some of our other distance calculation tools:

• Distance calculator;

• 2D distance calculator;

• Coordinate distance calculator;

• Euclidean distance calulator; and

• Distance between two points calculator.

The length of the line segment is 5. To obtain this result:

1. Use the distance formula:
   d = √[(x₂ - x₁)² + (y₂ - y₁)²]

2. In our example, the variables of this formula are:
   (x₁, y₁) = (0, 0)
(x₂, y₂) = (-3, 4)

3. Substitute and perform the corresponding calculations:
   d = √[(-3 - 0)² + (4 - 0)²]
d = √[(-3)² + (4)²]
d = √[9 + 16]
d = √25

4. By finding the square root of this number, you get the segment's length:
   d = 5