Cofunction Calculator
Welcome to Omni's cofunction calculator, where we'll study the cofunction identities and how to use them. In essence, in trigonometry, there are six functions that fully describe the relations between the angles and sides of a triangle. As such, they are connected to one another, so we often think of them as pairs: sin and cos, tan and cot, sec, and csc. Today we'll look into those relations and learn how to go from one map to its pair, i.e., its cofunction.
So sit back, relax, and enjoy some good mathematics!
Trigonometric functions
Before we see what a cofunction is, we need to start with the basics. And in geometry, we can't go more basic than triangles: three sides, three vertices, three inside angles. In some sense, there can be no simpler polygon.
We, however, are most interested in a particular type of triangle: right triangles (you know, the ones that the Pythagorean theorem is all about). One of their angles is always (hence, the name), so we already have some information about our shape even before we draw it.
Moreover, we can observe some other dependencies that make the triangle look the way it does. After all, if we increase one of the acute angles, we can easily see that the opposite side will have to get longer too. This observation is, more or less, the idea behind trigonometry: to somehow relate a triangle's inside angles to its sides. We focused on that topic in our trigonometry calculator.
We define trigonometric functions as ratios between a right triangle's sides. Below you can find a picture with the formulas for all six of them. (Note how in the cofunction calculator, there's one identity for each of them.)
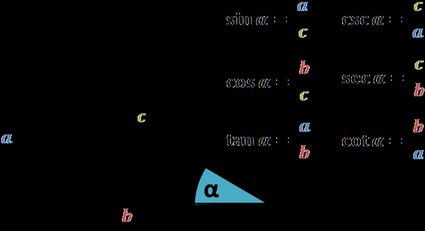
🔎 Trigonometric functions (sin, cos, tan) are all ratios. Therefore, you can find the missing terms using nothing else than our ratio calculator!
For instance, we see that the sine is equal to the leg opposite the angle divided by the hypotenuse. Observe how we never mention how big the triangle is. In fact, that's where a crucial property of trigonometry lies: even if we scale the triangle to twice its size, if we keep the angles intact, the values of the trigonometric functions will not change.
However, the above formulas, with all their grace, have a major flaw. We've defined them using a right triangle, so the angle can only be between and degrees (or and in radians). But don't sulk! Fortunately for us, for mathematics, and the whole world, there is a way to fix it! The only thing we need to do is translate the reasoning to a two-dimensional Euclidean space, i.e., the plane.
Let be a point on the plane, and define to be the angle going counterclockwise from the positive half of the horizontal axis to the line segment whose endpoints are and . (Note how we said that goes from one line to the other and not that it's just the angle between them. That's why we often call a directed angle.)
Obviously, can now be larger than . In fact, it can even go beyond . For such angles, we just consider the first to be the first lap around , and from that value, we continue with the second one (and, if need be, the third, fourth, etc.). In fact, it's even more than that - can also be negative. After all, we said that it's a directed angle, so for negative values, we simply reverse the direction, i.e., go clockwise instead of counterclockwise.
Now that we understand angles of all sizes, we can define the trigonometric functions for them and the point . The rule here is quite simple: we repeat the formulas from the figure above, but substitute for , for , and for , i.e., the distance from to . For example, the secant will now take the form:
Alright, we got to know trigonometric functions from the point of their definitions, so we're ready to dig deeper. After all, the name "cofunction calculator" is what brought us here, and we still don't know how to find a cofunction. For that, the best means is through the functions' graphs.
The cofunction graphs: sin and cos, tan and cot, sec and csc
The six trigonometric functions are sine and cosine (denoted and ), tangent and cotangent ( and ), and secant and cosecant ( and ).
You may already see why we paired them the way we did from the names alone. In each couple, we have the "basic" function and a map with the same name but with an additional prefix "co-". The resemblance to the word "cofunction" is far from coincidental. In each of the pairs, we say that one is the cofunction of the other.
"But what does it mean to be a cofunction?" Well, we're glad you asked! We'll see the cofunction identities in detail in the next section. First, however, let's try to motivate them by looking at the functions' graphs in pairs and spotting the similarities.
We begin with sine and cosine.
They look almost the same, don't they? The sine is just the cosine moved by (or in radians) to the right.
For our purposes, let's focus on the area from to and imagine that you're traveling this distance along the slopes of both curves but in different directions: the sine from to and the cosine from to . Can you see that the paths are then the same?
Speaking of slopes, the slope calculator can help you understand this concept and show how to find it. Be sure to check it if you're in need!
Let's try to do something similar for the tangent and cotangent graphs.
Again, if we trace the tangent curve from to , and the cotangent from to , we'll notice that we're going along a similar path.
Lastly, we have the sec and csc functions.

As you might have guessed, the story repeats itself for the secant and cosecant.
In essence, this is what characterizes cofunctions. We could say that their graphs are mutual reflections if we put a mirror in the midpoint of the interval, i.e., at . This, in turn, means that the value of a trigonometric function at should be the same as the cofunction's value at point . And this is precisely what the cofunction identities state.
Cofunction identities
As mentioned in the previous section, we divide trigonometric functions into pairs. In each, one is the cofunction of the other. This means that their graphs (and hence, values) are mutual reflections in the interval . Therefore, the value of the first at point is the same as the other at for from the interval.
If you'd like to please a few big-headed scientists, we can write the above paragraph equivalently using mathematical notation. It'd look like so:
However, remember that they work only for angles between and . The above formulas rely on the fact that the angles to either side of the sign are complementary, i.e., they sum up to .
In fact, there is a way to consider other angles as well. It is, however, tricky. Here, we had the convenience that all the functions admit positive values in the interval . Outside it, things can become negative. Also, there appears the issue of where to put "the mirror," which reflects the cofunctions.
Despite the obstacles, through hours of hard work, mathematicians were able to come up with formulas that generalize the cofunction identities. They are called the trigonometric reduction formulas (not the concept described in the power reducing calculator, mind you). Although we won't give them here, we happily encourage you to look them up and enjoy some extra mathematical knowledge. It certainly beats scrolling through social media if you ask us.
And with that, we declare the end of theory for today! Arguably, we've spent quite some time learning definitions and formulas. Why not take on some examples, and put the cofunction identities to good use?
Example: using the cofunction calculator
Say that you've decided to do some remodeling in your living room. After all, there's at least one silver lining to the coronavirus lockdown — you have a lot of time on your hands.
Your plan is to fix the flooring and maybe replace the tiles with wood. The problem is that you need the measurements, and the room is not a perfect rectangle; there are a couple of slant walls. Fortunately, you still remember a thing or two from college, and after some head-scratching, you realize that you'll need the cosine of and the cotangent of for further calculations.
There is an issue, though. It's been a few years since your last trigonometry lesson, and you can't recall the formulas for the cosine or cotangent. What you do remember are the sine and the tangent. Oh, how well the cofunction identities calculator fits into this scenario!
(Alright, we admit that the details are a little far-fetched, but please, give us a break. The imagination of Omni's content developers can only stretch so far.)
First of all, let's see how easy the task is when we have the cofunction calculator at hand. There, we begin by choosing the function that we have. Firstly, we choose the cosine, i.e., , from the list. Once we have that, we move to the variable field below, which contains the angle. We input from our problem, and the moment we do that, the cofunction calculator will spit out the answer underneath: the cofunction along with the value. Similarly, for the second case, we choose the cotangent () from the list and input .
Observe how each time the tool gives us a precise value (i.e., in the form of a fraction with square roots) apart from the rounded-up one. We will explain why it is so in a second. Also, although the cofunction calculator strives for precision, you might want to reduce the number of significant figures in the answer for any further calculations.
Now, let's leave Omni's tool aside and see how to find the answer ourselves. We will follow the steps below:
- Draw a right triangle with the angle given;
- Use cofunction identities to transform the function we're seeking into its cofunction; and
- Calculate the value of the cofunction by taking the ratios of the triangle's sides.
We begin with the angle.
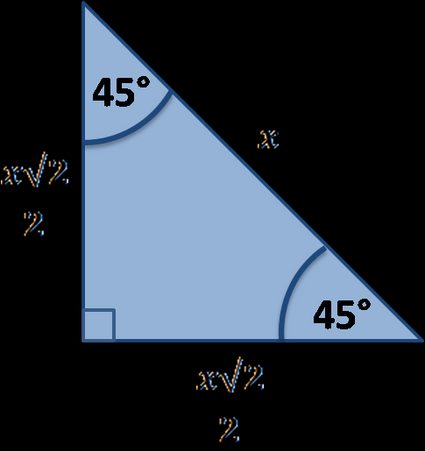
Observe that it's an example of quite a special triangle in which we know the relations between the sides, i.e., we know that if the leg is of length , then the hypotenuse must be . This is because our shape is, in fact, half of a square, where the long side is the square's diagonal. The special right triangles calculator can tell you more about this type of triangle.
Now, we recall the cofunction identities from the previous section and use them to transform into a sine:
This way, we can use the sine formula to find the answer. In the first section, we said that it's the leg opposite the angle divided by the hypotenuse. That gives:
We move on to the case. Again, we start with a drawing.

As before, we're fortunate enough to know the relations between the sides. This time, it's because our shape is, in fact, half of an equilateral triangle.
We use the cofunction identities to transform into a tangent:
Note that although the angle in question changed, we can still use the same picture. This will always be the case with cofunction identities since we're always dealing with complementary angles, that is, ones that form the acute angles of the same right triangle.
Lastly, we recall the tangent formula from the first section: the function returns the leg opposite the angle divided by the other one. In our case, this is:
Done! We found the trigonometric functions we needed; we're ready to take care of these tiles and upgrade the living room. Surely, it will be so much cozier once you install plywood. And when you're done, why not go further and figure something out for the bedroom?
FAQs
How do I use the cofunction identities?
Cofunction identities allow you to determine the value of a trigonometric function given the value of the cofunction (of your function) at the angle that is complementary to your angle. For instance, you can easily find cos(20°) if you know sin(70°) because sine and cosine are cofunctions and 70° + 20° = 90°.
What is x for which sin(x) = cos(15°) holds?
The answer is x = 75°. We know that sine and cosine are cofunctions, i.e., their values agree on complementary angles. So, x and 15° must be complementary: x + 15° = 90°. Hence, x = 75°, as claimed.
How do I find sine with cosine?
To determine sin(x) given cos(x), follow these steps:
- Compute the square of
cos(x). - Subtract
cos²(x)from1. - Take the square root of the result from Step 2. Remember, there are two possible results: one positive and one negative.
- What you've got are the two possible values of
sin(x). If you know, e.g., that your anglexis acute, then its sine is positive. - The full form of the formula we've applied is
sin²(x) + cos²(x) = 1.
How do I find sine with cosine and tangent?
To determine the sine of an angle given its cosine and tangent, you need to multiply cosine by tangent. The formula you need is:
sin(α) = tan(α) × cos(α)