Last updated: Oct 29, 2024

Trajectory Calculator

Q: What is the trajectory of a projectile launched at 30° at 10 m/s?

Assuming a launch with zero initial height , the trajectory of the projectile follows this equation: y = (x × tan(30°)) + (g × x²)/(2 × 10² × cos²(30°))

Q: What is the shape of the trajectory of a projectile?

The trajectory followed by a projectile is a parabola , hence a quadratic equation in the horizontal coordinate. This motion is a consequence of the action of the force of gravity: a deceleration in the vertical direction transfers a quadratic dependence on the vertical movement.

New

Table of contents

Trajectory definition Trajectory formula Trajectory calculator: how to use FAQs

Use this trajectory calculator to find the flight path of a projectile. Type in three values: velocity, angle, and initial height, and in no time, you'll find the trajectory formula and its shape. Keep reading if you want to check the trajectory definition as well as a simple example of calculations.

While you are here, be sure to check out our projectile motion calculator as well.

Trajectory definition

Trajectory, also called a flight path, is the path followed by a moving object under the action of gravity. Usually, we use the term when talking about projectiles or satellites (where the regularly repeating trajectory is called an orbit). If you were to throw an object for a short distance, then a parabola is a good approximation of trajectory shape.

Some examples of projectile motion are:

Ice hockey puck, baseball, or golf ball in flight ⚾.
A bullet fired from a weapon 🔫.
A jet of water from a fountain ⛲.
Blood droplets. (Why? Check our angle of impact calculator).
Object is thrown from a table / plane / building / bridge ✈️.

Trajectory formula

Now that you know the trajectory definition, let's check what the trajectory formula looks like.

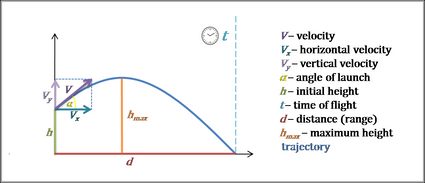
Projectile motion image. Velocity, angle of launch, initial height, time of flight, distance and maximum height marked

1. Let's start with equations of motion:

\qquad x = V_x \times t

\qquad y = h +V_y \times t - \frac{g\times t^2}{2}

2. As we know that three vectors — $V_0$ , $V_x$ , and $V_y$ — form a right triangle, we can write that:

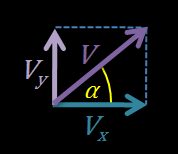
Velocity and its horizontal and vertical component

The horizontal velocity component $V_x$ is equal to $V_0\times \cos(\alpha)$ .
The vertical velocity component $V_y= V_0\times \sin(\alpha)$ .

3. Then, we combine the equations of motion and velocity components into one formula:

\qquad \begin{split} x &= V_x\times t\\ t & = \frac{x}{V_x} \end{split}

Hence:

\begin{split} y &= h +V_y \times t - \frac{g\times t^2}{2}\\[1.5em] y &= h +V_y \times \frac{x}{V_x} - \frac{g\times( \frac{x}{V_x})^2}{2}\\[1.5em] y &= h+x\times\frac{V_0\times \sin(\alpha)}{V_0\times \cos(\alpha)}\\[1.5em] &\quad-g\times\frac{1}{2}\times\left(\frac{x}{V_0\times\cos(\alpha)}\right)^{\!2} \end{split}

And as we know, sine over cosine is a definition of a tangent. So, the final trajectory formula may be expressed as:

\begin{split} y &= h+x\times\tan(\alpha)\\[1.5em] &-g\times \frac{x^2}{2\times V_0^2 \times\cos^2(\alpha)} \end{split}

If you're interested in different aspects of projectile motion, check out our other tools:

Trajectory calculator: how to use

Let's check out the trajectory of water from a water fountain:

Bubbler. Example of trajectory in projectile motion

Type in the velocity. Assume that it's equal to $5\ \mathrm{ft/s}$ .
Enter the angle. For example, $60\degree$ .
Choose initial height. Let's pick $5\ \mathrm{in}$ .
Here you are! Trajectory calculator displays the formula and the flight path!

The critical thing to notice is the possible difference in axes scaling, so the angle may not look the way it should on the chart. Remember that in all calculations, air resistance is neglected.

FAQs

How do I find the maximum angle in the projectile motion?

To find the angle that maximizes the horizontal distance in the projectile motion, follow the next steps:

Take the expression for the traveled horizontal distance: x = sin(2θ) × v²/g.
Differentiate the expression with regard to the angle: 2 × cos(2θ) × v²/g.
Equate the expression to 0 and solve for θ: the angle which gives 0 is 2θ = π/2; hence θ = π/4 = 45°.

What is the trajectory of a projectile launched at 30° at 10 m/s?

Assuming a launch with zero initial height, the trajectory of the projectile follows this equation:

y = (x × tan(30°)) + (g × x²)/(2 × 10² × cos²(30°))

What is the shape of the trajectory of a projectile?

The trajectory followed by a projectile is a parabola, hence a quadratic equation in the horizontal coordinate. This motion is a consequence of the action of the force of gravity: a deceleration in the vertical direction transfers a quadratic dependence on the vertical movement.

How do I calculate the maximum height of a projectile with θ = 40° and v₀=5 m/s?

To calculate it:

Start from the equation for the vertical motion of the projectile: y = vᵧ × t - g × t² / 2, where vᵧ is the initial vertical speed equal to vᵧ = v₀ × sin(θ) = 5 × sin(40°) = 3.21 m/s.
Calculate the time required to reach the maximum height: it corresponds to the time at which vᵧ = 0, and it is equal to t = vᵧ/g = 3.21 / 9.81 = 0.327 s.
Substitute the values in the equation:
y = 3.21 × 0.327 - 9.81 × (0.327)² /2 = 0.525 m.