Last updated: Apr 02, 2024

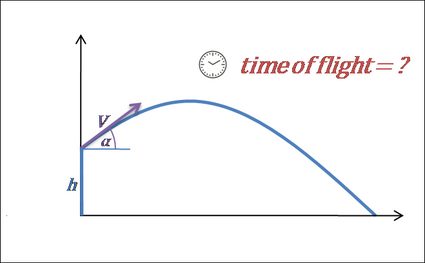
Time of Flight Calculator – Projectile Motion

Q: What is a time of flight sensor?

The time of flight (ToF) sensor measures the distance between two points using the ToF principle using light or sound . A signal, usually light photons, is sent from the sensor's emitter to the target and then received back at the sensor receiver. The time taken by the signal helps measure the distance. Typical applications include robot navigation, obstacle detection, and vehicle monitoring . Read more

Table of contents

Time of flight equation Time of flight exemplary calculations FAQs

With this time of flight calculator, you can easily calculate the time the projectile remains in the air. To solve this particular case of projectile motion, all you need to enter are the initial velocity, angle, and height. Read on to learn more about the time of flight equations, or simply play with the calculator instead!

Time of flight equation

If you throw a ball or shoot an arrow in the air, it will follow a parabolic path before hitting the ground. Visit the projectile motion calculator if you'd like to learn about it in more detail. Below we'll explain how to find out how long this movement would last.

To define the time of flight equation, we should split the formulas into two cases:

1. Launching projectile from the ground (initial height = 0).

Let's start with an equation of motion:

y = V_{0}\,t\sin(\alpha) - \frac{1}{2}gt^2,

where:

$V_0$ – Initial velocity;
$t$ – Time since start of flight;
$\alpha$ – Angle of the initial flight path; and
$g$ – Acceleration due to gravity.

The flight ends when the projectile hits the ground (y = 0).

0 = V_0\,t\sin(\alpha) - \frac{1}{2}gt^2

Then, $t$ is the time of flight – the total time of the whole journey:

t = \frac{2V_0\,\sin(\alpha)}{g}

Note that the air resistance is neglected.

Which angle of launch causes the projectile to spend the most time in the air? Let's have a look at the final time of flight equation again: the higher the value of sine is, the longer the time in the air. The maximum value of sine occurs when the angle = 90°. So if you throw an object upwards, it will keep moving for the longest time.

Additionally, if the velocity is equal to 0, then it's the case of a free fall. You can explore the concept of free fall further in our free fall calculator.

2. Launching projectile from some height (initial height > 0).

However, if the projectile is thrown from some elevation $h$ , the formula is a bit more complicated:

\footnotesize t = \frac{V_0\sin(\alpha) + \sqrt{(V_0 \sin(\alpha))^2 + 2gh}}{g}

You can also estimate the path the projectile will follow using the trajectory calculator. Not only that but there's also the projectile range calculator, allowing you to see how far it would go!

Time of flight exemplary calculations

Let's use this time of flight calculator to find out how long it takes for a pebble thrown from the edge of the Grand Canyon to hit the ground.

Type in the velocity value. Assume it's 16 ft/s.
Enter the angle – for example, 20°. If you choose angle = 0°, it would be the example of horizontal projectile motion.
Finally, type in the initial height. Let's take the deepest point of the Canyon. It's a 6,000 ft difference – over a mile! Type this value into our tool.
The time of flight calculator will show you the total time the pebble remains in the air. It's 19.5 seconds for our example.

All the calculations are made without taking into account air resistance. In reality, the trajectory would differ from the ideal parabola, and the range would be shorter than the result obtained from the calculations.

FAQs

How can I calculate time of flight?

You may calculate the time of flight of a projectile using the formula:

t = 2 × V₀ × sin(α) / g

where:

t – Time of flight;
V₀ – Initial velocity;
α – Angle of launch; and
g – Gravitational acceleration.

What is the time of flight equation?

You can measure the time of flight in two instances; first, when the object is launched from the ground, i.e., height equals zero. Second when the object is launched from a certain height.

Height, h = 0:

t = 2 × V₀ × sin(α) / g
h > 0:

t = [V₀ × sin(α) + √((V₀ × sin(α))² + 2 × g × h)] / g

where:

t – Time of flight;
V₀ – Initial velocity;
α – Angle of launch;
h – Height; and
g – Gravitational acceleration.

What is time of flight in physics?

A projectile launched into the air stays in the air for some time before coming to the ground. The time it remains in the air is called the time of flight. The object could be in the form of light or sound waves as well.

Interestingly, the time of flight principle also helps determine the distance between objects in sensitive environments.

What is a time of flight sensor?

The time of flight (ToF) sensor measures the distance between two points using the ToF principle using light or sound.

A signal, usually light photons, is sent from the sensor's emitter to the target and then received back at the sensor receiver. The time taken by the signal helps measure the distance.

Typical applications include robot navigation, obstacle detection, and vehicle monitoring.

Velocity

Angle of launch

Initial height

Time of flight

Velocity components

Check out 26 similar kinematics calculators — how things move ⏱️

Arrow speedBallistic coefficientCar jump distance...23 more