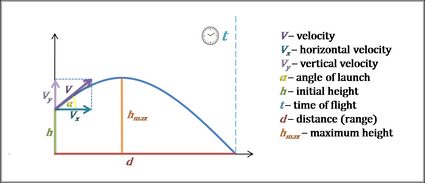
Projectile Motion Calculator

Our projectile motion calculator is a tool that helps you analyze parabolic projectile motion. It can find the time of flight, but also the components of velocity, the range of the projectile, and the maximum height of flight. Continue reading if you want to understand what projectile motion is, get familiar with the projectile motion definition, and determine the abovementioned values using the projectile motion equations.

Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you:

Imagine an archer sending an arrow in the air. It starts moving up and forward, at some inclination to the ground. The further it flies, the slower its ascent is — and finally, it starts descending, moving now downwards and forwards and finally hitting the ground again. If you could trace its path, it would be a curve called a trajectory in the shape of a parabola. Any object moving in such a way is in projectile motion. By the way, we have the arrow speed calculator that analyzes the motion of arrows — give it a try!

Only one force acts on a projectile — the gravity force. Air resistance is always omitted. If you drew a free-body diagram of such an object, you would only have to draw one downward vector and denote it “gravity”. If there were any other forces acting on the body, then — by projectile motion definition — it wouldn't be a projectile.

Projectile motion is pretty logical. Let's assume you know the initial velocity of the object $V$, the angle of launch $\alpha$, and the initial height $h$. Our projectile motion calculator follows these steps to find all remaining parameters:

1. Calculate the components of velocity.

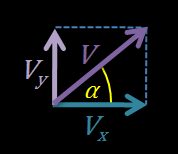
• The horizontal velocity component $V_\mathrm x$ is equal to $V \cos\alpha$.
• The vertical velocity component $V_\mathrm y$ is equal to $V \sin\alpha$.
• Three vectors — $V$, $V_\mathrm x$ and $V_\mathrm y$ — form a right triangle.

If the vertical velocity component is equal to 0, then it's the case of horizontal projectile motion. If, additionally, α = 90°, then it's the case of free fall. We tackled both problems in the horizontal projectile motion calculator and free fall calculator, respectively.

2. Write down the equations of motion.

Distance

• Horizontal distance traveled can be expressed as $x = V_\mathrm x t$ where $t$ is the time.
• Vertical distance from the ground is described by the formula $y = h + V_\mathrm{y0} t - g t^2 / 2$, where $g$ is the gravity acceleration and $V_\mathrm{y0}$ is the initial vertical velocity.

Velocity

• Horizontal velocity is equal to $V_\mathrm x$.
• Vertical velocity can be expressed as $V_\mathrm y = V_\mathrm{y0} - g t$.

Acceleration

• Horizontal acceleration is equal to 0.
• Vertical acceleration is equal to $-g$ (because only gravity acts on the projectile).

3. Calculate the time of flight.

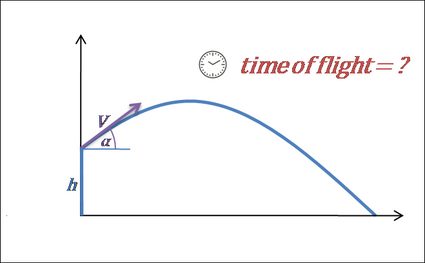
• Flight ends when the projectile hits the ground. We can say that it happens when the vertical distance from the ground is equal to 0. In the case where the initial height is 0, the formula can be written as: $V_\mathrm{y0} t - g t^2 / 2 = 0$. Then, from that equation, we find that the time of flight is

• However, if we're throwing the object from some elevation, then the formula is not so nicely reduced as before, and we obtain a quadratic equation to solve: $h + V_\mathrm{y0} t - g t^2 / 2 = 0$. After solving this equation, we get:

4. Calculate the range of the projectile.

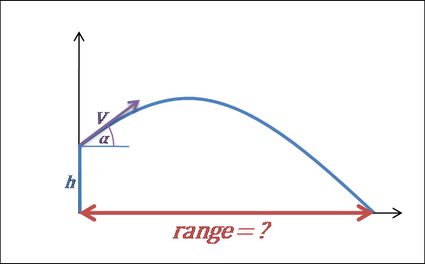
• The range of the projectile is the total horizontal distance traveled during the flight time. Again, if we're launching the object from the ground (initial height = 0), then we can write the formula as $R = V_\mathrm x t = V_\mathrm x \times 2 \times V_\mathrm{y0} / g$. It may be also transformed into the form: $R = V^2_0 \sin(2\alpha) / g$

• Things are getting more complicated for initial elevation differing from 0. Then, we need to substitute the long formula from the previous step as $t$:

• The range is especially important in ballistics. We talked about it more in detail in the ballistic coefficient calculator.

5. Calculate the maximum height.

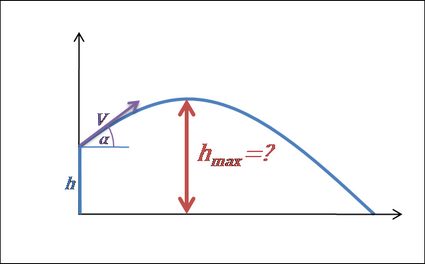
• When the projectile reaches the maximum height, it stops moving up and starts falling. It means that its vertical velocity component changes from positive to negative — in other words, it is equal to 0 for a brief moment at time $t(V_\mathrm y=0)$.
• If $V_\mathrm {y0} - g t(V_\mathrm y=0) = 0$, then we can reformulate this equation to $t(V_\mathrm y=0) = V_\mathrm{y0} / g$.
• Now, we simply find the vertical distance from the ground at that time:

• Fortunately in the case of launching a projectile from some initial height $h$, we need to simply add that value into the final formula:

Uff, that was a lot of calculations! Let's sum that up to form the most essential projectile motion equations:

1. Launching the object from the ground (initial height h = 0):

• Horizontal velocity component: $V_\mathrm x = V_0 \cos \alpha$
• Vertical velocity component: $V_\mathrm y = V_0 \sin \alpha - gt$
• Time of flight: $t = 2 V_\mathrm{y0} / g$
• Range of the projectile: $R = 2 V_\mathrm x V_\mathrm{y0} / g$
• Maximum height: $h_\mathrm{max} = V^2_\mathrm{y0} / (2 g)$

2. Launching the object from some elevation (initial height h > 0):

• Horizontal velocity component: $V_\mathrm x = V_0 \cos \alpha$
• Vertical velocity component: $V_\mathrm y = V _0 \sin \alpha - gt$
• Time of flight: $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Range of the projectile: $R = V_\mathrm x \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Maximum height: $h_\mathrm{max} = h + V^2_ \mathrm{y0} / (2 g)$

Using our projectile motion calculator will surely save you a lot of time. It can also work 'in reverse'. For example, enter the time of flight, distance, and initial height, and watch it do all the calculations for you!

Be sure also to check the parabola calculator to learn more about such a curve from a mathematical point of view.