Maximum Height Calculator - Projectile Motion
The maximum height calculator is a tool for finding the maximum vertical position of a launched object in projectile motion. Whether you need the max height formula for an object starting directly off the ground or from some initial elevation - we've got you covered. If you're still wondering how to find maximum height of a projectile, read the two short paragraphs below, and everything should become clear.
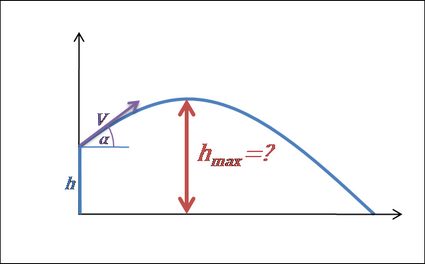
How to find the maximum height of a projectile?
Maximum height of the object is the highest vertical position along its trajectory. The object is flying upwards before reaching the highest point - and it's falling after that point. It means that at the highest point of projectile motion, the vertical velocity is equal to 0 (Vy = 0).
0 = Vy – g * t = V₀ * sin(α) – g * th
From that equation we can find the time th needed to reach the maximum height hmax:
th = V₀ * sin(α) / g
The formula describing vertical distance is:
y = Vy * t – g * t² / 2
So, given y = hmax and t = th, we can join those two equations together:
hmax = Vy * th – g * th² / 2
hmax = V₀² * sin(α)² / g – g * (V₀ * sin(α) / g)² / 2
hmax = V₀² * sin(α)² / (2 * g)
And what if we launch a projectile from some initial height h? No worries! Apparently, the calculations are a piece of cake - all you need to do is add this initial elevation!
hmax = h + V₀² * sin(α)² / (2 * g)
Let's discuss some special cases with changing angle of launch:
-
if α = 90°, then the formula simplifies to:
hmax = h + V₀² / (2 * g)and the time of flight is the longest.If, additionally, Vy = 0, then it's the case of free fall. Also, you may want to have a look at our even more accurate equivalent - the free fall with air resistance calculator.
-
if α = 45°, then the equation may be written as:
hmax = h + V₀² / (4 * g)and in that case, the range is maximal if launching from the ground (h = 0). -
if α = 0°, then vertical velocity is equal to 0 (Vy = 0), and that's the case of horizontal projectile motion. As sine of 0° is 0, then the second part of the equation disappears, and we obtain :
hmax = h- initial height from which we're launching the object is the maximum height in projectile motion.
Maximum height calculator helps you find the answer
Just relax and look how easy-to-use this maximum height calculator is:
- Choose the velocity of the projectile. Let's type 30 ft/s.
- Enter the angle. Assume we're kicking a ball ⚽ at an angle of 70°.
- Optionally, type the initial height. In our case, our starting position is the ground, so type in 0. Can the ball fly over a 13-ft fence?
- Here it is - maximum height calculator displayed the answer! It's 12.35 ft. So it will not fly over the mentioned barrier - throw it harder or increase the angle to reach your goal.
Just remember that we don't take air resistance into account!
