Last updated: May 21, 2024

Polar Moment of Inertia Calculator

Q: What are the units of polar moment of inertia?

The polar moment of inertia units typically used are mm 4 in the International System of Units and in 4 in the United States customary system. These are also the units for the first and second area moments.

Q: What is the difference between the area moment of inertia and the polar moment of inertia?

The polar moment of inertia is a geometrical property used to predict how easily a circular beam in torsion will deform and how high the shear stress will be. A higher polar moment of inertia implies lower shear stress and deformation. The area moment of inertia is a geometrical property that indicates how easily a beam deflects and how high the normal stress is under bending. More moment of inertia translates into lower deflection and lower normal stress.

Q: What is the polar moment of inertia of a circle of diameter 5 cm?

61.36 cm 4 . To calculate the polar moment of inertia J of a circle of diameter D = 5 cm , use the formula: J = πD ⁴/32 = π (5 cm)⁴/32 = 61.36 cm⁴ . You can also use our polar moment of inertia calculator.

Created by Luis Hoyos

Luis Hoyos

Luis Hoyos is a fresh graduate Mechanical Engineer with thermodynamics and fluids mechanics expertise. He's interested in learning new things and applying them to real-life problems. Luis also likes to build tools that make repetitive and boring tasks a breeze, like calculators (surprise?). When he's not creating calculators, he's in the process of building the size of the tissue attached to his bones, aka bodybuilding. He also loves being with his little cat and seeing her do crazy things. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

Why do we need the polar moment of inertia?Formula: solid circle polar moment of inertia Formula: hollow cylinder polar moment of inertia How do I calculate the polar moment of inertia?FAQs

If you're searching for how to calculate the polar moment of inertia (also known as the second polar moment of area) of a circular beam subjected to torsion, you're in the right place.

The polar moment of inertia and second moment of area are two of the most critical geometrical properties in beam analysis. The polar moment is essential for analyzing circular elements subjected to torsion (also known as shafts), while the area moment of inertia is for parts subjected to bending.

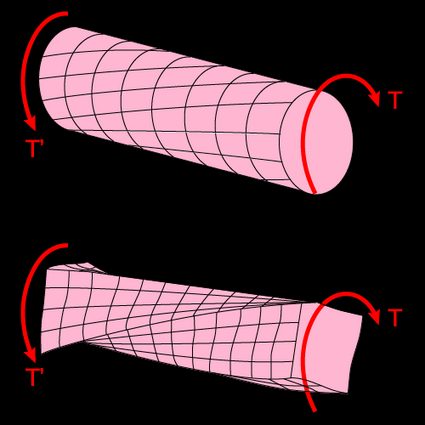
Torsion-subjected members are widely present in engineering applications involving power transmission. The most common is the driveshaft in automobile drivetrains used to transmit power to the drive wheels. Similarly, transmission shafts are used in power generation to send the energy from turbines to electric generators. Independently of the amount of transmitted power, it'll be mandatory to calculate the stresses and deformations in those shafts to avoid mechanical failure. For the latter, you'll need the polar moment.

In the following sections, you can learn about the polar moment of inertia formulas for a hollow and a solid circle. We'll explain why we cannot use them to analyze noncircular beams.

🙋 Once you've calculated the polar moment of inertia, you can use it in our shear stress calculator to find the stress caused by a torque applied to a circular beam. On the other hand, our section modulus calculator can be helpful if you're dealing with bending.

Why do we need the polar moment of inertia?

The polar moment of inertia relates to the stress and resistance to deformation in beams subjected to a specific torsional load. In circular beams, we can connect it mathematically to the shear stress and angle of twist in the following ways:

Shear stress: the shear stress due to torsion in a circular shaft is given by:

\tau = \frac{T\rho}{J}

, where:

$J$ — Polar moment of inertia;
$T$ — Torque applied to the beam;
$\rho$ — Radial distance from the shaft axis to the point where we want to calculate the shear stress; and
$\tau$ — Shear stress at radial distance $\rho$ .

Angle of twist: the angle of twist due to torsion in a circular shaft equals:

\phi = \frac{TL}{JG}

, where:

$\phi$ — Angle of twist (in radians);
$L$ — Shaft length; and
$G$ — Shear modulus of the shaft material.

🔎 Once you've calculated the polar moment of inertia, you can obtain $\phi$ with our angle of twist calculator.

Mathematically, the polar moment of inertia is the sum of all the area differentials of a cross-section times their respective squared distances about a defined axis.

J = \int_A \rho^2dA

$J$ is equivalent to the second moment of area about the z-axis ( $I_z$ ), and, thanks to the perpendicular axis theorem, we can relate it to the second area moment of the other two axes:

J = I_z = I_x + I_y

We can solve this integral or apply the perpendicular axis theorem for many different shapes and obtain their polar moment. Unfortunately, we cannot use the obtained solutions to calculate $\tau$ and $\phi$ in noncircular cross-sections. The previous equations relating $\tau$ and $\phi$ to $J$ are derived assuming the cross-section of the member remains plane and undistorted in the presence of torque, which only occurs in circular sections.

Comparison of the deformations obtained in circular and rectangular bars. — Comparison of the deformations obtained in circular and rectangular bars under torsion.

Formula: solid circle polar moment of inertia

If the beam or shaft has a cross-section with the form of a solid circle, we can solve the previous integral about the centroidal axis of the circular section and obtain the following:

J = \frac{\pi}{2}R^4

, where:

$J$ polar moment of the beam; and
$R$ beam radius.

You can express this formula in terms of the diameter ( $D$ ), remembering that $R = D/2$ :

J = \frac{\pi}{32}D^4

Formula: hollow cylinder polar moment of inertia

Solving the integral for a hollow circular section, the polar moment of inertia formula is:

J = \frac{\pi}{2}(R^4-{R_i}^4)

where $R_i$ is the inner beam radius.

You can also express this formula in terms of the outer ( $D$ ) and inner diameter ( $d$ )

J = \frac{\pi}{32}(D^4-{d}^4)

How do I calculate the polar moment of inertia?

To calculate the polar moment of inertia:

Define if you want the polar moment of inertia of a solid or a hollow circle.
For a solid circular section, use the polar moment of inertia formula J = πR⁴/2, where R is the radius, and J is the polar moment of inertia.
For a hollow circle, the polar moment of inertia is given by J = π(R⁴ - Rᵢ⁴)/2, where Rᵢ is the inner radius.

FAQs

What are the units of polar moment of inertia?

The polar moment of inertia units typically used are mm⁴ in the International System of Units and in⁴ in the United States customary system. These are also the units for the first and second area moments.

How do I calculate the polar moment of inertia of an ellipse?

The equivalent to the polar moment of inertia of an ellipse is its torsion constant. To calculate the torsion constant of an ellipse, use the formula:

K = πa³b³/(a² + b²)

, where:

K – Torsion constant of the ellipse;
a – Distance between the center and any ellipse vertexes; and
b – Distance between the center and the other ellipse's vertexes.

You can use K to calculate the angle of twist but not to find the shear stress.

What is the difference between the area moment of inertia and the polar moment of inertia?

The polar moment of inertia is a geometrical property used to predict how easily a circular beam in torsion will deform and how high the shear stress will be. A higher polar moment of inertia implies lower shear stress and deformation.
The area moment of inertia is a geometrical property that indicates how easily a beam deflects and how high the normal stress is under bending. More moment of inertia translates into lower deflection and lower normal stress.

What is the polar moment of inertia of a circle of diameter 5 cm?

61.36 cm⁴. To calculate the polar moment of inertia J of a circle of diameter D = 5 cm, use the formula: J = πD⁴/32 = π(5 cm)⁴/32 = 61.36 cm⁴. You can also use our polar moment of inertia calculator.

How do I calculate the polar moment of inertia of a hollow cylinder?

To calculate the polar moment of inertia of a hollow cylinder, use the formula:

J = π(R⁴ - Rᵢ⁴)/2

, where:

J – Cylinder polar moment of inertia;
R – Cylinder outer radius; and
Rᵢ – Cylinder inner radius.