Shear Modulus Calculator

Welcome to our shear modulus calculator, where you'll be able to calculate the shear modulus of a cubic element subjected to a force tangent to its area.

The shear modulus, also known as the modulus of rigidity, is a material property used in many applications. For example:

• In our shear strain calculator, the shear modulus is necessary to find the shear strain due to shear stress.
• It's also needed to calculate the angle of twist in shafts subjected to torsion.
• From the theoretical point of view, it has great relevance, as shear modulus, Young's modulus, and Poisson's ratio are the constants that form the generalized Hook's law for homogenous isotropic materials.

Read on to learn the modulus of rigidity equation used by this calculator and the modulus of rigidity of steel and many other materials.

Although an idealization, Hooke's law is a powerful tool for studying the behavior of materials that follow a linear stress-strain relationship. In a material subjected to shear stress, this law takes the form:

, where:

• $\tau$ — Shear stress;
• $G$ — Shear modulus; and
• $\gamma$ — Shear strain.

In this linear equation, the modulus of rigidity is the proportionality constant. A higher shear modulus implies we'll need to apply higher shear stress to get the same deformation.

A typical example of shear stress is the cubic element in the following image, subjected to a force tangent to its surface.

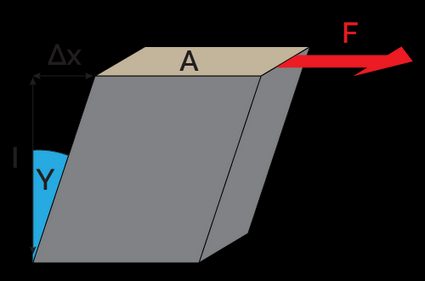
• Shear stress is the quotient of the force and the surface area $A$ over which that force $F$ is applied: $\tau = \frac{F}{A}$.
• Shear strain is the angle $\gamma$ owing to the deformation $\Delta x$. This angle is usually very tiny, and we can approximate it to $\gamma = \frac{\Delta x}{l}$.

Inputting the previous expressions into $\tau = G\gamma$ and solving for $G$, we finally get the shear modulus formula used by this calculator:

Sometimes, we know the material to use in advance and don't need a modulus of rigidity equation. In that case, here are the shear modulus values of common materials:

• Aluminum: 25 GPa (3.6 × 10⁶ psi).
• Brass: 35 GPa (5.1 × 10⁶ psi).
• Copper: 44 GPa (6.4 × 10⁶ psi).
• Iron: 77 GPa (3.8 × 10⁶ psi).
• Lead: 6 GPa (0.87 × 10⁶ psi).
• Silicone rubber: 0.002 GPa (0.00029 × 10⁶ psi).
• Steel: 75 GPa (10.9 × 10⁶ psi).

For specific materials used in engineering, look at the following table:

The modulus of rigidity unit is the pascal (Pa) in the International System of Units and pound per square inch (psi) in the United States customary units system. The modulus of rigidity of materials is typically so large that we express it in gigapascals (GPa) instead of Pascals.