Last updated: Jun 07, 2024

Shear Strain Calculator

Q: What is the unit of shear strain?

The shear strain unit is radian , a dimensionless unit. For this reason, the shear strain unit is often omitted. Besides, the normal strain unit is also radians or dimensionless.

Q: How to calculate shear strain?

To calculate the shear strain γ , divide the shear stress 𝜏 by the shear modulus G . For example, in a brass element ( G = 3.5×10¹⁰ Pa ) subjected to a shear stress of 𝜏 = 8.0×10⁶ Pa , shear strain equals γ = (8.0×10⁶ Pa)/(3.5×10¹⁰ Pa) = 2.3×10⁻⁴ . That's how to calculate shear strain! You can also use our shear strain calculator.

Q: Which is the shear strain symbol?

The shear strain symbol is the Greek letter γ , gamma. Depending on the direction and plane of actuation of the stress, γ can have different subscripts: The shear strain symbol γ xy represents the strain in the XY plane caused by the shearing stresses 𝜏 xy and 𝜏 yx . γ yz represents the same in the YZ plane, caused by 𝜏 yz and 𝜏 zy , the stresses in that plane. γ zx represents the same in the ZX plane, caused by the 𝜏 yz and 𝜏 zy stresses.

Q: How to calculate the modulus of rigidity in a torsion test?

To calculate the modulus of rigidity G in a torsion test: Organize the list of angles of twist (in radians) corresponding to each torque applied. Plot each torque (vertical axis) against its corresponding angle (horizontal axis). Get the slope of the part of the graph that follows a linear relationship. As torque T and angle of twist ϕ relate each other linearly by the equation: T = ( JG / L ) ϕ , to get G , equal the slope of the graph to JG / L , and solve for G . The result would be G = slope × L / J .

Q: How to calculate the strain energy of shear stress?

To calculate the strain energy density for a material under plane shearing stress, use the equation u = 𝜏 ²/(2 G ) , where: 𝜏 — Shear stress applied to the material; G — Shear modulus of the material; and u — Strain energy density (energy per unit volume). To calculate the total strain energy of shear stress U , integrate the strain energy density through the entire volume V : U = ∫[ 𝜏 ²/(2 G )] d V

Created by Luis Hoyos

Luis Hoyos

Luis Hoyos is a fresh graduate Mechanical Engineer with thermodynamics and fluids mechanics expertise. He's interested in learning new things and applying them to real-life problems. Luis also likes to build tools that make repetitive and boring tasks a breeze, like calculators (surprise?). When he's not creating calculators, he's in the process of building the size of the tissue attached to his bones, aka bodybuilding. He also loves being with his little cat and seeing her do crazy things. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

Shear strain definition How to calculate shear strain Max shear strain formula for a shaft under torsion What is the unit of shear strain?FAQs

This shear strain calculator finds the strain due to shearing stresses in different situations (shear force or torque).

Shear stresses act in almost every mechanical situation, and the strain energy of these shear stresses is a powerful tool for solving deflection problems using energy methods. For this reason, it's essential to be aware of shear strain and the equations behind it.

If you're interested in knowing where things come from, in the following sections, we present the shear strain equations behind this calculator and the max shear strain formula for a shaft under torsion.

Shear strain definition

Suppose you apply two tangent forces on the opposite faces of a cubic or rectangular element. If that occurs, one of the faces will displace a distance $x$ relative to the other.

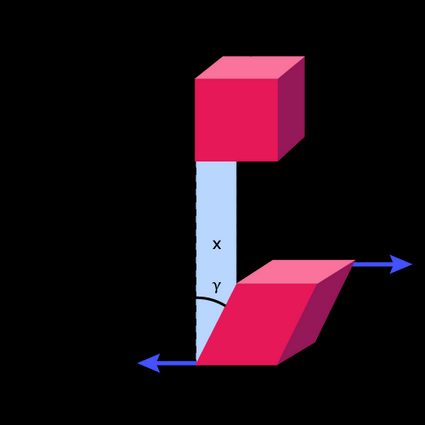
Image of a cubic element subjected to shear force.

The shear strain is no more than the angle $\gamma$ (shown in the image) caused by the displacement $x$ . In practice, displacement $x$ is much smaller than $h$ , and $\gamma$ is a small angle.

How to calculate shear strain

Depending on the situation and the information available, you'll need a different equation to calculate the shear strain.

Cubic object with known displacement

If we know the displacement $x$ , we can calculate the shear strain with the following formula:

\gamma = \frac{x}{h}

, where:

$\gamma$ — Shear strain;
$x$ — Displacement due to shear stress caused by forces $F_{||}$ ; and
$h$ — Transverse dimension of the element, as shown in the previous image.

Strictly speaking, $x/h$ is not the shear strain ( $\gamma$ ) but the tangent of the shear strain. Even so, we can say $x/h$ and ( $\gamma$ ) are practically the same, as for small $\gamma$ angles, $\tan(\gamma) \approx \gamma$

Element with known shear modulus subjected to shear stress

We usually don't know the displacement $x$ due to shear stress, and when that occurs, we can calculate the shear strain this way:

\gamma = \frac{\tau}{G}

, where:

$\tau$ — Shear stress applied to the element; and
$G$ — Shear modulus, also known as modulus of rigidity, of the material.

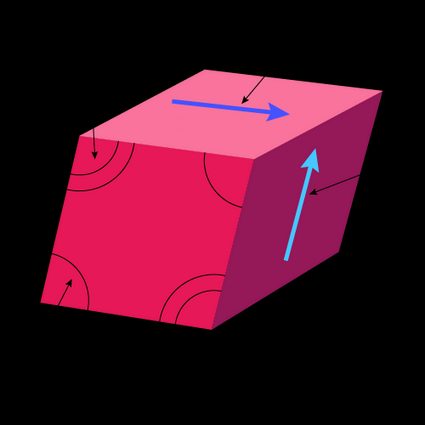
Image of an element subjected to shear stress.

Contrary to the previous case, this formula provides the angle $\gamma$ instead of its tangent.

💡 This equation is a version of Hooke's law expressed in terms of shear stress and strain. You can use our shear stress calculator to obtain the shear stress under different situations.

🔎 Besides Poisson's ratio and the Elastic modulus, these three constants help to form the group of equations representing the general form of Hooke's law for homogenous isotropic materials.

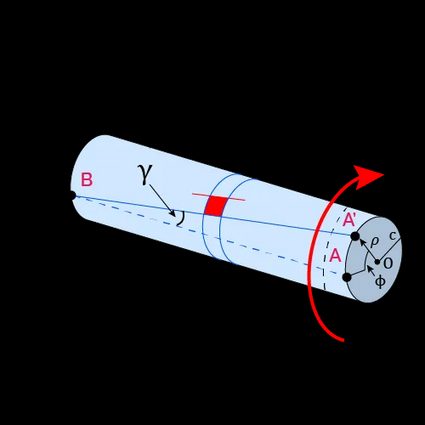
Circular shaft subjected to torsion

When we apply a torque to a circular shaft, every element parallel and perpendicular to the shaft axis suffers shear strain. We can calculate this shear strain with the formula:

\gamma = \frac{\rho\, \phi}{L}

where:

$\rho$ — Distance from the axis to the point at which we want to know the shear strain;
$\phi$ — Angle of twist of the transverse section (obtain it with the angle of twist calculator); and
$L$ — Length of the shaft.

Image of a circular shaft subjected to torsion. — A and A' are the initial and final positions of a specific point before and after the applied torsion.

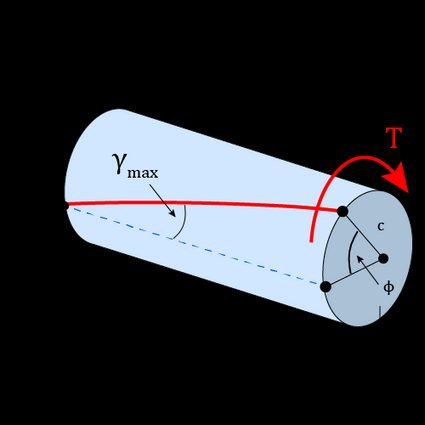
Max shear strain formula for a shaft under torsion

As you can note from the previous formula, a greater $\rho$ implies a higher strain. At the shaft surface, where $ρ$ equals the shaft radius ( $c$ ), the shear strain is maximum:

\gamma_{max} = \frac{c\, \phi}{L}

Image describing the maximum shear strain in a circular shaft subjected to torsion.

What is the unit of shear strain?

The shear strain unit is radian, a dimensionless unit. For this reason, the shear strain unit is often omitted. Besides, the normal strain unit is also radians or dimensionless.

FAQs

How to calculate shear strain?

To calculate the shear strain γ, divide the shear stress 𝜏 by the shear modulus G. For example, in a brass element (G = 3.5×10¹⁰ Pa) subjected to a shear stress of 𝜏 = 8.0×10⁶ Pa, shear strain equals γ = (8.0×10⁶ Pa)/(3.5×10¹⁰ Pa) = 2.3×10⁻⁴.

That's how to calculate shear strain! You can also use our shear strain calculator.

Which is the shear strain symbol?

The shear strain symbol is the Greek letter γ, gamma. Depending on the direction and plane of actuation of the stress, γ can have different subscripts:

The shear strain symbol γ_xy represents the strain in the XY plane caused by the shearing stresses 𝜏_xy and 𝜏_yx.
γ_yz represents the same in the YZ plane, caused by 𝜏_yz and 𝜏_zy, the stresses in that plane.
γ_zx represents the same in the ZX plane, caused by the 𝜏_yz and 𝜏_zy stresses.

How to calculate the modulus of rigidity in a torsion test?

To calculate the modulus of rigidity G in a torsion test:

Organize the list of angles of twist (in radians) corresponding to each torque applied.
Plot each torque (vertical axis) against its corresponding angle (horizontal axis).
Get the slope of the part of the graph that follows a linear relationship.
As torque T and angle of twist ϕ relate each other linearly by the equation: T = (JG/L)ϕ, to get G, equal the slope of the graph to JG/L, and solve for G. The result would be G = slope × L/J.

How to calculate the strain energy of shear stress?

To calculate the strain energy density for a material under plane shearing stress, use the equation u = 𝜏²/(2G), where:
- 𝜏 — Shear stress applied to the material;
- G — Shear modulus of the material; and
- u — Strain energy density (energy per unit volume).
To calculate the total strain energy of shear stress U, integrate the strain energy density through the entire volume V:

U = ∫[𝜏²/(2G)] dV