Section Modulus Calculator

Q: What are the units of the second moment of area?

The second moment of area units are mm⁴ or m⁴ in the International System of Units and in⁴ in the United States customary units. On the other hand, the elastic section modulus units are mm³ , m³ , and in³ .

Q: How to calculate the section modulus of a pipe pile?

To calculate the section modulus of a pipe pile of thickness t and radius R , use the section modulus formula for a very thin annulus: S = π R ² t , or follow these steps: Measure the radius R and the thickness t of the pipe pile. Multiply the number π by the square of the radius. Multiply the last result by the thickness. That's it! You can also use our section modulus calculator and do it faster. If the pipe is not very thin, you can calculate it using our section modulus calculator .

Q: What are the elastic section modulus units?

The elastic section modulus units are mm³ or m³ in the International System of Units and in³ in the United States customary units. Curiously, these are the same units of volume.

Q: What are the dimensions of a W6 x 12 beam?

The W6 x 12 dimensions are: Area: 3.55 in²; Dept: 6.03 in; Flange width: 4.00 in; Flange thickness: 0.280 in; and Web thickness: 0.230 in. Additionally, its second moment of area about the horizontal centroidal axis is 22.1 in⁴, while the elastic section modulus about the same axis is 7.31 in³.

Q: What is the section modulus formula for a rectangular section?

The elastic section modulus formula of a rectangle is S = bd ²/6 , where: S — Section modulus; d — Height of the rectangle; and b — Base or width of the rectangle. Take into account that this section modulus is about the horizontal centroidal axis. We can derive the section modulus formula for a rectangular section by dividing its second moment of area ( bh ³/12) by the maximum distance from the neutral axis ( h /2 ): S = (bh ³/12)/( h /2) = bh ²/6

Q: What is the section modulus formula for a square section?

The elastic section modulus formula of a square is S = a ³/6 , where: S — Section modulus; and a — The length of any of the square sides; We can derive the section modulus formula for a square section by dividing its second moment of area ( a ⁴/12 ) by the maximum distance from the neutral axis ( a /2 ): S = ( a ⁴/12)/( a /2) = a ³/6

Q: How do I calculate the plastic section modulus of an I-section?

To calculate the plastic section modulus of an I-section , use the formulas: Zₓ = 0.25 d ² t ᵥᵥ + bt(d + t) Zᵧ = 0.5 b ² t + 0.25 dtᵥᵥ ² where: Zₓ — Plastic section modulus about the horizontal plastic neutral axis; Zᵧ — Plastic section modulus about the vertical plastic neutral axis; d — Web length; t ᵥᵥ — Web thickness; t — Flange thickness; and b — Flange length.

Creators

Luis Hoyos

Luis is a mechanical engineer who works at Omni Calculator as a content creator and researcher specializing in math and physics calculators with a focus on thermodynamics and classical mechanics. With a strong foundation in mechanical engineering, Luis is passionate about creating tools that simplify complex concepts and improve everyday life. Outside of work, Luis likes weightlifting and applying his engineering knowledge to optimize the thermal conditions of his home, all while caring for four beloved cats. See full profile

Check our editorial policy

Reviewers

Steven Wooding

Steven Wooding is a physicist by training with a degree from the University of Surrey specializing in nuclear physics. He loves data analysis and computer programming. He has worked on exciting projects such as environmentally aware radar, using genetic algorithms to tune radar, and building the UK vaccine queue calculator. Steve is now the Editorial Quality Assurance Coordinator here at Omni Calculator, making sure every calculator meets the standards our users expect. In his spare time, he enjoys cycling, photography, wildlife watching, and long walks. See full profile

Check our editorial policy

New

This tool calculates the section modulus, one of the most critical geometric properties in the design of beams subjected to bending. Additionally, it calculates the neutral axis and area moment of inertia of the most common structural profiles (if you only need the moment of inertia, check our moment of inertia calculator)

The formulas for the section modulus of a rectangle or circle are relatively easy to calculate. Still, when dealing with complex geometries like a tee, channel, or I beam, a calculator can save time and help us avoid mistakes.

In the following sections, we discuss the two types of section modulus, how to calculate section modulus from the moment of inertia, and present the section modulus formulas of a rectangle and many other common shapes.

How to calculate section modulus from the moment of inertia

The section modulus is used by engineers to quickly predict the maximum stress a bending moment will cause on a beam. The equation for the maximum absolute value of the stress in a beam subjected to bending:

\sigma_m = \frac{Mc}{I}

where:

$\sigma_m$ — Maximum absolute value of the stress in a specific beam section;
$M$ — Bending moment to which the beam is subjected in that section;
$c$ — Largest distance from the neutral axis to the surface of the member; and
$I$ — Second moment of area (also known as area moment of inertia) about the section neutral axis (also calculated by this tool).

For example, in a circle, the largest distance equals the radius, while it equals half the height in a rectangle.

As the ratio $I/c$ only depends on the geometric characteristics, we can define a new geometric property from it, called the section modulus, denoted by the $S$ letter:

S = \frac{I}{c}

As well as the second moment of area, this new geometric property is available in many tables and calculators, but if you want to know how to calculate section modulus from the moment of inertia, simply divide $I$ by $c$ , and you'll get it.

Finally, we can relate the section modulus to the stress and moment:

\sigma_m = \frac{M}{S}

🙋 Does this relationship seem familiar to you? This relation is equivalent to the axial stress equation: $\sigma = \frac{F}{A}$ . The bending moment is analogous to axial force, while the section modulus is analog to the cross-sectional area. You can use our stress calculator to obtain the axial stress.

Take these considerations into account when calculating section modulus and maximum stresses:

We obtain the bending moment through a static or structural analysis of the beam.
To get the section modulus, we can use tables for predefined structural members, but this calculator is the best option if you're dealing with custom geometries.
If we're considering a uniform section beam (as usual), the location of the maximum stress will be at the point of maximum bending moment. If that's not the case, $\sigma_m$ could be at a different place.
The previous formulas apply to materials that exhibit an elastic behavior and obey Hook's law. When there's plastic deformation instead of elastic deformation, we need to use the plastic section modulus.

Plastic section modulus: beyond elastic section modulus

The previous equations don't apply when we subject a beam material to stresses beyond the yield strength, as they assume stress and strain are linearly related. In this case, we must use the plastic section modulus. Similar to the elastic section modulus $S$ , its plastic counterpart provides a relationship between stress and moment:

M_p = Z\sigma_Y

where:

$M_p$ — Plastic moment of the section;
$Z$ — Plastic section modulus; and
$\sigma_Y$ — Yield strength of the member material.

The plastic moment refers to the moment required to cause plastic deformation across the whole transverse area of a section of the member.

The usefulness of the last equation is that we can predict the bending moment that will cause plastic deformation by just knowing the yield strength and plastic section modulus.

The following graphic better describes what we refer to when talking about plastic moments:

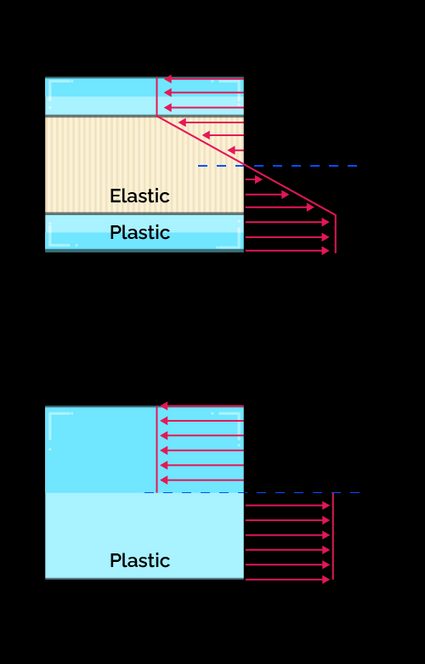
Image of the stress distribution during plastic deformation — Graphic representation of the bending stress distribution during plastic deformations. We're assuming a perfect plasticity model; therefore, actual stress distributions are not that uniform.

For plastic deformation to occur, we must cause some stress equal to the yield strength of the material. As you can note, the transition from elastic to plastic is not uniform across the member, as some regions will reach the yield strength before others.

Once all the section reaches the yield strength, plastic deformation occurs across all that section. The bending moment needed to achieve this is called the plastic moment.

Section modulus formulas for a rectangular section and other shapes

In the following table, we list the section modulus formula for a rectangular section and many other profiles (scroll the table sideways to see all the equations):

Form		Elastic section Modulus
Square		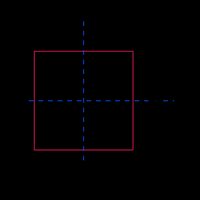$y_c = x_c = a/2$
		$I_x = I_y = \frac{a^4}{12}$
		$S_x = S_y =\frac{I_x}{y_c} = \frac{a^3}{6}$

Rectangle		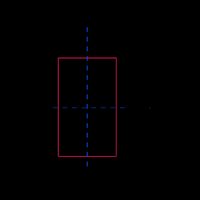$y_c=d/2$
		$x_c=b/2$
		$I_x = \frac{bd^3}{12}$
		$I_y = \frac{db^3}{12}$
		$S_x = \frac{I_x}{y_c} = \frac{b d^2}{6}$
		$S_y = \frac{I_y}{x_c} = \frac{d b^2}{6}$

Hollow rectangle (rectangular tube)		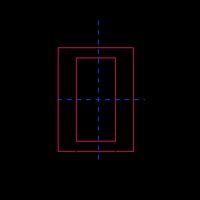$y_c=d/2$
		$x_c=b/2$
		$I_x = \frac{bd^3-b_id_i^3}{12}$
		$I_y = \frac{db^3-d_ib_i^3}{12}$
		$S_x = \frac{I_x}{y_c}$
		$S_y = \frac{I_y}{x_c}$

Tee section		$y_c=\frac{bt^2+t_wd(2t+d)}{2(tb+t_wd)}$
		$x_c=b/2$
		$A = tb + t_wd$
		$I_x = \frac{b(d+t)^3-d^3(b-t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ - \footnotesize A(d+t-y_c)^2$
		$I_y = \frac{tb^3+dt_w^3}{12}$
		$S_x = \frac{I_x}{d+t-y_c}$
		$S_y = \frac{I_y}{x_c}$

Channel section		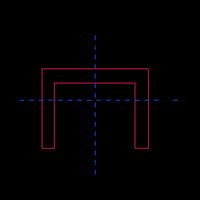$y_c=\frac{bt^2+2t_wd(2t+d)}{2(tb+2t_wd)}$
		$x_c=b/2$
		$I_x = \frac{b(d+t)^3-d^3(b-2t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ -\footnotesize A(d+t-y_c)^2$
		$I_y = \frac{(d+t)b^3-d(b-2t_w)^3}{12}$
		$S_x = \frac{I_x}{d+t-y_c}$
		$S_y = \frac{I_y}{x_c}$
		$A = tb + 2t_wd$

Wide-flange beam (equal flanges)		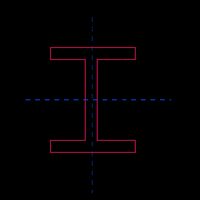$y_c=d/2+t$
		$x_c=b/2$
		$I_x = \frac{b(d+2t)^3-(b-t_w)d^3}{12}$
		$I_y = \frac{b^3t}{6} + \frac{t_w^3d}{12}$
		$S_x = \frac{I_x}{y_c}$
		$S_y = \frac{I_y}{x_c}$

Angle		$y_c=\frac{d^2+bt+-t^2}{2(b+d-t)}$
		$x_c=\frac{b^2+dt-t^2}{2(b+d-t)}$
		$A = t(b+d-t)$
		$\footnotesize I_x = \frac{bd^3-(b-t)(d-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(d-y_c)^2$
		$\footnotesize I_y = \frac{db^3-(d-t)(b-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(b-x_c)^2$
		$S_x = \frac{I_x}{d-y_c}$
		$S_y = \frac{I_y}{b-x_c}$
		$A = t(b+d-t)$

Circle		$y_c = x_c = R$
		$I_x = I_y = \frac{\pi}{4}R^4$
		$S_x = S_y =\frac{I_x}{y_c} = \frac{\pi}{4}R^3$

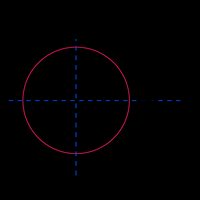Hollow circle or pipe		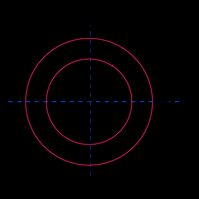$y_c = x_c = R$
		$I_x = I_y = \frac{\pi}{4}(R^4-R_i^4)$
		$S_x = S_y =\frac{I_x}{y_c}$

🔎 Are you interested in calculating deflections instead of stresses? We have a beam deflection calculator.

What are the units of the second moment of area?

The second moment of area units are mm⁴ or m⁴ in the International System of Units and in⁴ in the United States customary units. On the other hand, the elastic section modulus units are mm³, m³, and in³.

FAQs

How to calculate the section modulus of a pipe pile?

To calculate the section modulus of a pipe pile of thickness t and radius R, use the section modulus formula for a very thin annulus: S = πR²t, or follow these steps:

Measure the radius R and the thickness t of the pipe pile.
Multiply the number π by the square of the radius.
Multiply the last result by the thickness.
That's it! You can also use our section modulus calculator and do it faster.

If the pipe is not very thin, you can calculate it using our section modulus calculator.

What are the elastic section modulus units?

The elastic section modulus units are mm³ or m³ in the International System of Units and in³ in the United States customary units. Curiously, these are the same units of volume.

What are the dimensions of a W6 x 12 beam?

The W6 x 12 dimensions are:

Area: 3.55 in²;
Dept: 6.03 in;
Flange width: 4.00 in;
Flange thickness: 0.280 in; and
Web thickness: 0.230 in.

Additionally, its second moment of area about the horizontal centroidal axis is 22.1 in⁴, while the elastic section modulus about the same axis is 7.31 in³.

What is the section modulus formula for a rectangular section?

The elastic section modulus formula of a rectangle is S = bd²/6, where:

S — Section modulus;
d — Height of the rectangle; and
b — Base or width of the rectangle.

Take into account that this section modulus is about the horizontal centroidal axis.

We can derive the section modulus formula for a rectangular section by dividing its second moment of area (bh³/12) by the maximum distance from the neutral axis (h/2):

S = (bh³/12)/(h/2) = bh²/6

What is the section modulus formula for a square section?

The elastic section modulus formula of a square is S = a³/6, where:

S — Section modulus; and
a — The length of any of the square sides;

We can derive the section modulus formula for a square section by dividing its second moment of area (a⁴/12) by the maximum distance from the neutral axis (a/2):

S = (a⁴/12)/(a/2) = a³/6

How do I calculate the plastic section modulus of an I-section?

To calculate the plastic section modulus of an I-section, use the formulas:

Zₓ = 0.25d²tᵥᵥ + bt(d + t)
Zᵧ = 0.5b²t + 0.25dtᵥᵥ²

where:

Zₓ — Plastic section modulus about the horizontal plastic neutral axis;
Zᵧ — Plastic section modulus about the vertical plastic neutral axis;
d — Web length;
tᵥᵥ — Web thickness;
t — Flange thickness; and
b — Flange length.