Lever Calculator

Q: What is the lever equation?

The lever equation defines the forces and the physical features of a lever in its equilibrium status. It derives from the comparison of the torque acting on the lever: Fa × a = Fb × b where: Fᵢ are the forces, either the effort or the resistance; and lᵢ are the arms of the lever ( a and b ). Manipulate that simple equation to isolate the desired quantity. Read more

Q: How long should the arm of a lever be to balance a 1500 kg car with my weight?

Let's say you weigh 70 kg . To balance a car with a mass of 1500 kg , you can use a lever defined by the mechanical advantage: MA = (1500 × g)/(70 × g) = 21.43 where g is the standard gravitational parameter, equal to 9.81 m/s² . The arm of the lever on your side should be 21.43 times longer than the arm on the car side. Read more

Q: How to calculate the mechanical advantage of a lever?

You can calculate a lever's mechanical advantage by computing the ratio of the forces acting on the lever or, interchangeably, the ratio of the lever's arms: MA = Fa/Fb = a/b The mechanical advantage can be smaller, greater, or equal to one. Read more

Q: What is the mechanical advantage of a lever?

The mechanical advantage of a lever tells you if the lever you are using will give you an edge when doing some mechanical work. A mechanical advantage greater than 1 defines levers that help you lift heavy loads. In contrast, a mechanical advantage smaller than 1 defines levers that reduce the force you apply, but instead return an increased speed. Read more

Created by Davide Borchia

Reviewed by Anna Szczepanek, PhD and Jack Bowater

Last updated: Jan 18, 2024

Table of contents:

Archimedes said, "Give me a lever long enough" – use our lever calculator to find out how long that lever should be!

Here you will learn:

The physics behind levers and the lever equation;
The law of the lever, by Archimedes;
What is the mechanical advantage of a lever; and
Some examples of levers in action, both practical and impractical!

What is a lever?

A lever is probably the most straightforward mechanism ever devised by humanity. Take a plank of wood (or any rigid material), find a place where to put it, and you are all set.

Regardless of their lack of complexity, levers are marvelous machines everywhere in our daily lives. Look around you wherever you are: scissors, nail clippers, bottle openers, and so on, are all levers. Let's discover more about them.

🔎 Levers appear all the time in nature, in particular in the animal kingdom. Muscles, joints, jaws: evolution engineered the living being to be as good as possible.

A lever allows you to move an object with a specific advantage – that is, you'll be able to move it with either a reduced effort or an increased speed or displacement.

Levers work thanks to the application of forces and the exploitation of the torques which derive from them. This alters the balance, allowing us to lift heavy loads with very little effort.

The elements of a lever

We can describe levers with a relatively small number of elements:

Fulcrum;
Effort; and
Resistance.

The fulcrum is where the lever pivots. The fulcrum doesn't need to be in the middle of the lever – in fact, its position allows for entirely different uses of this simple machine. You can learn more about it with our fulcrum calculator.

The resistance (or load) is the force applied by the object you want to move, cut, or whatever else your lever does. We identify the resistance with the symbol $F_b$ . The segment between the fulcrum to the point of application of the resistance is denoted as $b$ .

The effort is the force you apply when operating the lever. The distance from the point of application to the fulcrum is $a$ , while its value is $F_a$ .

The lever equation

The operational principle of a lever is straightforward. We can identify an equilibrium situation where the lever is stationary.

In that condition, the torque applied to the lever by both forces equal each other.

The torque is the rotational analog of a linear force and, in layman's words, describes the effect of a force $F$ applied at a certain distance $x$ (the arm) from a pivot:

\boldsymbol{\tau}= \mathbf{x}\times\mathbf{F}= x\times F\times \sin{\theta}

The quantities are in bold because we need to consider them as vectors: the torque's magnitude depends on the sine of the angle between the applied force and the arm.

Good news! In a lever, the angle $\theta$ is usually equal to $90\degree$ , and we can happily ignore it since $\sin{90\degree}=1$ . To learn more about torque, check out our torque calculator!

Back to the equilibrium condition. We said that the torques equal each other:

\tau_a = a \times F_a = b \times F_b = \tau_b

This equation allows us to find out every quantity we need in a problem involving levers. For example, if the arms' length is known, it is possible to calculate the force required to attain equilibrium against a specific resistance.

The mechanical advantage of a lever and the law of the lever

The quantity that measures the "performance" of a lever is called mechanical advantage. It derives from analyzing the torque applied by both forces on the lever.

The famous law of the lever says that the multiplication of the force in a lever is given by:

\text{MA} = \frac{F_a}{F_b} = \frac{a}{b}

Take a look at the formula and remember that $a$ corresponds to the side where you apply the effort and $b$ relates to the resistance.

First thing: it is easier to think in terms of the arms and not the forces: it is pretty obvious that the greater the force you apply, the higher the mechanical advantage is. But imagine now having a really "unbalanced" lever, with the effort applied at a distance far greater than the one of the resistance: $a\gg b$ .

The mechanical advantage of such a lever would be extremely high, reflected in the need to apply a really high effort on one of the levers.

🔎 Archimedes said: "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world". He had in mind a lever with a particularly good mechanical advantage!

The value of the mechanical advantage tells us how the lever behaves. The higher the mechanical advantage, the smaller the effort applied to balance the same resistance. In that case, the lever is called a force multiplier.

If the mechanical advantage equals $1$ , the lever gives you no edge: it would be like applying the effort directly. Finally, if the mechanical advantage is smaller than $1$ , the lever is a speed multiplier, which means you'll move the point where the resistance is applied faster than you'd think for the effort (over the same time, hence increasing the speed).

🙋 We dedicated an entire calculator to the mechanical advantage in various simple machines – check it out at our mechanical advantage calculator!

The three types of levers

How the various elements of a lever relate to one another allows us to define three different types of levers:

Class I levers – The levers we picture in our mind when someone asks us to think of one. The fulcrum is between resistance and effort.
Class II levers – The resistance and the effort are placed on the same side on the same side of the fulcrum, with $a>b$ .
Class III levers – The resistance and the effort are placed on the same side of the fulcrum, but this time $a<b$ .

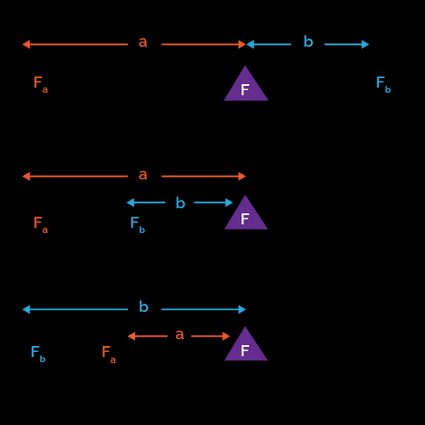
Levers types — The three types of levers. From the top, a **class I** lever, a **class II** lever, and a **class III** lever.

Now we know how to characterize them. Let's take a look at the possible mechanical advantages!

For a class I lever, $a$ and $b$ can take every possible value greater than $0$ (and bounded by the length of the lever, of course). According to the ratio of $a$ and $b$ , such a lever can be a force multiplier.
For a class II lever, $a\text{\textgreater}b$ . This implies that the mechanical advantage is greater than $1$ , and the lever always acts as a force multiplier.
For a class III lever, the opposite is true. Since $b\text{\textgreater} a$ the mechanical advantage is always smaller than $1$ , and so the lever always acts as a speed multiplier.

An example: calculate the lever arm to lift the world

We can calculate the characteristics of a lever able to lift the world using the lever equation. There's only a condition: you're the one doing the lifting!

Assuming a weight of $70\ \text{kg}$ and that you're standing on your end of the lever, we can compute an effort of:

\footnotesize F_a=70\ \text{kg}\times9.81\ {\text{m/}}{\text{s}^2} = 686.7\ \text{N}

What about the Earth? Eehh... its mass is $M_E=5.9722\times10^{24}\ \text{kg}$ , which corresponds to a resistance of:

\footnotesize \begin{align*} F_b &=5.9722\times10^{24}\ \text{kg}\times9.81\ {\text{m/}}{\text{s}^2}\\ &= 5.8587\times10^{25}\ \text{N} \end{align*}

We need to consider a lever long enough: let's say as long as the distance between the Earth and the Sun ( $148.81\times10^9\ \text{m}$ ). Calling the length $l$ , and using the equality $a = l-b$ , we can write the equation of the lever as:

l-b=\frac{F_b\times b}{F_a}

Let's isolate $b$ :

\begin{align*} (l-b)\times F_a &= b\times F_b\\\\ l\times F_a &= (F_a + F_b)\times b\\\\ b&=\frac{l\times F_a}{F_a+F_b} \end{align*}

This equation allows us to find the length of the lever's arm associated to the resistance, in our case, the Earth. We substitute the numerical values (neglecting $F_a$ at the denominator), and we calculate the arm of the lever:

\footnotesize \begin{align*} b&=\frac{1.481\times 10^{11}\ \text{m} \times 687.7\ \text{N}}{5.8587\times 10^{25}\ \text{N}}\\\\ &=1.74\times10^{-12}\ \text{m} \end{align*}

That's one long lever: the arm on which the Earth rests is smaller than a hydrogen atom!

A lever to lift the world — Our Archimedes is trying to lift the world using only a lever. Will he manage doing so?

Back to some more practical examples that don't involve lifting planets. Let's say you are at the playground, playing on the seesaw with one of your friends. By now, you know that the seesaw is a class I lever. We assume that your weight is $75\ \text{kg}$ and your friend, being on the thin side, is only $60\ \text{kg}$ .

The seesaw is $4\ \text{m}$ long. Where do you have to sit to balance your friend? And what is the mechanical advantage of the lever you created?

Apply the lever equation to find the arm of your side of the lever. Notice that in the equation you can use the masses instead of the weights. They differ only by the multiplicative constant, $g$ , the standard gravitational parameter, and we can cancel it out.

\footnotesize \begin{align*} a&=\frac{g\times 60\ \text{kg}\times 2\ \text{m}}{g\times 75\ \text{kg}}\\\\ &=\frac{60\ \text{kg}\times 2\ \text{m}}{75\ \text{kg}}=1.6\ \text{m} \end{align*}

You have to seat $40\ \text{cm}$ before the end of the seesaw to equal your friend's resistance – now the game is... balanced!

Now we can calculate the lever's mechanical advantage. Calculate the quotient of the two arms' lengths

\text{MA}=\frac{a}{b}=\frac{1.6\ \text{m}}{2\ \text{m}} = 0.8

It is smaller than $1$ because you are lifting a smaller weight than yours.

How to calculate the mechanical advantage of a lever using our lever calculator

Our lever calculator is a helpful tool that allows you to calculate everything you need in your physics homework — and not only: we hope that it can help you in your everyday problems too!

Leverage your time and quickly find the results: insert the quantities you know, and find the results. You can insert the forces acting on the levers, the arms, or the mechanical advantage and only one of the other quantities, to find the remaining ones!

FAQ

What is the lever equation?

The lever equation defines the forces and the physical features of a lever in its equilibrium status. It derives from the comparison of the torque acting on the lever:

Fa × a = Fb × b

where:

Fᵢ are the forces, either the effort or the resistance; and
lᵢ are the arms of the lever (a and b).

Manipulate that simple equation to isolate the desired quantity.

How long should the arm of a lever be to balance a 1500 kg car with my weight?

Let's say you weigh 70 kg. To balance a car with a mass of 1500 kg, you can use a lever defined by the mechanical advantage:

MA = (1500 × g)/(70 × g) = 21.43

where g is the standard gravitational parameter, equal to 9.81 m/s². The arm of the lever on your side should be 21.43 times longer than the arm on the car side.

How to calculate the mechanical advantage of a lever?

You can calculate a lever's mechanical advantage by computing the ratio of the forces acting on the lever or, interchangeably, the ratio of the lever's arms:

MA = Fa/Fb = a/b

The mechanical advantage can be smaller, greater, or equal to one.

What is the mechanical advantage of a lever?

The mechanical advantage of a lever tells you if the lever you are using will give you an edge when doing some mechanical work. A mechanical advantage greater than 1 defines levers that help you lift heavy loads. In contrast, a mechanical advantage smaller than 1 defines levers that reduce the force you apply, but instead return an increased speed.

Davide Borchia

Effort (Fa)

Effort's arm (a)

Resistance (Fb)

Resistance's arm (b)

Mechanical advantage

Belt lengthBrake Mean Effective Pressure (BMEP)Carburetor CFM… 20 more