Last updated: Aug 05, 2024

Fulcrum Calculator

Q: How do you find the fulcrum point?

To calculate the fulcrum location of a lever of length L , follow these steps: Determine the class of the lever based on the location of the fulcrum , the load F r , and the effort F e . Calculate the mechanical advantage MA using the equation MA = F r /F e . For a class I lever , calculate the distance d r of the fulcrum from the load using d r = L / (MA + 1) . For a class II lever , determine the distance d r of the fulcrum from the load using d r = L / MA . For a class III lever , the distance d r of the fulcrum from the load is equal to the length of the lever, d r = L .

Q: Which fulcrum position on a 1m lever can give twice the mechanical advantage?

1/3 m away from the load and 2/3 m away from the effort . To calculate the fulcrum position that gives a mechanical advantage of MA = 2 with a class I lever of length L = 1 m , follow these simple steps: Calculate the distance d r from the load to the fulcrum using d r = L/( MA + 1) = 1/3 . Determine the distance d e from the fulcrum to the effort using d e = L - d r = 1 - 1/3 = 2/3 . Verify your results using our fulcrum calculator.

Q: What type of lever is the human elbow joint?

The human elbow joint is an example of a Class III lever . When we lift loads in our fists, the elbow joint acts as a fulcrum and the bicep muscle exerts the needed force a small distance from the elbow.

Q: How do you calculate the length of the effort arm?

To calculate the length of the effort arm d e of a lever to lift a load F r with an effort F e , follow these simple steps: Determine the mechanical advantage MA using MA = F r /F e . Measure the length of the load arm d r as the distance between the fulcrum and the load. Multiply MA with d r to get the effort arm as d e = MA × d r .

Created by Krishna Nelaturu

Krishna Nelaturu

Krishna holds a Master's degree in Applied Mechanics and never shies away from asking questions and digging deeper. He has two years of experience in steel castings and a particular fascination for vehicle dynamics. For his thesis, Krishna developed a new optimization method to reduce squeak and rattle in premium cars. He is passionate about mathematics and physics and constantly wonders about our place in the Universe. He also loves stories and storytelling and hopes to write a book someday. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is the fulcrum of a lever?Law of the lever and calculating mechanical leverage Types of levers Fulcrum equation How do you find the fulcrum point?How to use this lever fulcrum calculator FAQs

This fulcrum calculator with help you find the ideal fulcrum point on your lever so that you can lift a load or apply a force with the mechanical advantage you desire!

You've come to the right place if you were wondering how one chooses a lever's fulcrum position on one's lever. In this article, let's discuss the fundamental laws that calculate a lever fulcrum and answer these basic questions:

What is the fulcrum of a lever?
How do you calculate mechanical leverage?
What is the fulcrum equation for the three classes of levers?
How to find the fulcrum point?

If you're exclusively interested in calculating lever forces, use our lever calculator.

What is the fulcrum of a lever?

A lever is a simple machine made up of a beam or a bar that pivots around a point on itself. This pivot point is called its fulcrum or pivot point, and it usually connects the lever to the ground.

Aside from the beam (or bar) of your lever, there are three main components you need to know:

Fulcrum is the pivot point around which a lever rotates.
Resistance is the load we want to lift or apply force through our lever.
Effort is the force we shall apply to the lever to move it.

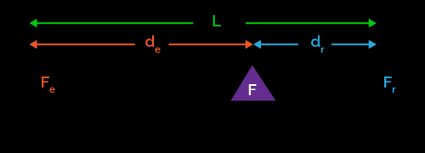
Free body diagram of a lever. — A length of bar pivoted at a fulcrum $F$ can be used to multiply the effort force $(F_e)$ to easily lift loads or move resistance $(F_r)$ .

Law of the lever and calculating mechanical leverage

The law of the lever states that the forces applied farther away from the fulcrum must be less than the forces applied closer to it. We can summarize this with a balance of moments to obtain:

F_r \cdot d_r = F_e \cdot d_e

where:

$F_r$ - Resisting force (or load);
$d_r$ - Distance of the resistance from the fulcrum (or the "load arm");
$F_e$ - Effort force that we apply to lift (or counterbalance) the resistance; and
$d_e$ - Distance of the effort from the fulcrum (or the "effort arm").

We use this lever equation for calculating lever forces. To understand the moments in a lever, we recommend you read further in our torque calculator.

A lever's mechanical leverage or the mechanical advantage is the ratio of the resisting force to the effort force. By combining with the lever equation we introduced above, we can calculate mechanical leverage as:

MA = \frac{F_r}{F_e} = \frac{d_e}{d_r}

Here $MA$ is the mechanical advantage.

This relation shows that we can lift heavy loads with little effort if the effort arm is longer than the load arm. To quote Archimedes, "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world."

If you wish to learn more about this, use our mechanical advantage calculator.

Types of levers

Before we proceed to the lever fulcrum calculation, we must learn the class of the lever. Based on the location of its three components, we can classify levers as follows:

Class I lever has the fulcrum between the load and the effort. A see-saw is the first image that should come to mind.
Class II lever has the resistance between the fulcrum and the effort. Wheelbarrows are an excellent example of this kind.
Class III lever has the effort between the fulcrum and the load. A pair of tongs and tweezers are great examples to visualize this class.

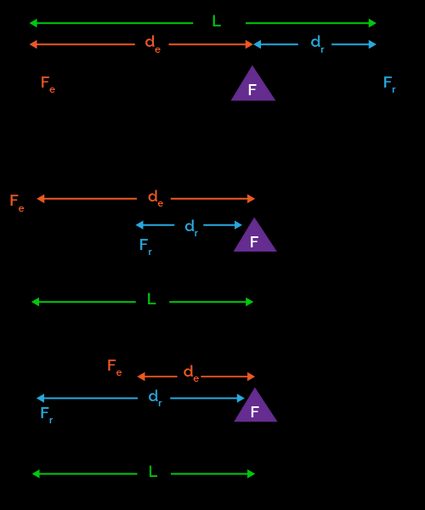
Classes of lever. — The three classes of lever shown in order.

Fulcrum equation

Say $L$ is the length of the lever at hand, and you need to calculate the fulcrum of the lever.

First, consult the previous section to decide which class of lever you have because it determines the type of the fulcrum equation we must use.

For Class I lever, the length of the lever is:

\qquad \begin{align*} L &= d_r + d_e\\ \implies d_e &= L - d_r \end{align*}

Substituting this in the lever equation, we get:

\qquad \begin{align*} d_r &= \frac{L}{\frac{F_r}{F_e}+1}\\[1.5em] \implies d_r &= \frac{L}{MA + 1} \end{align*}

We can use this fulcrum formula for calculating lever distances for all class I levers.

For Class II lever, the length of the lever is:

\kern{4.3em} L = d_e

In other words, the fulcrum and the effort are on the opposite ends of the lever. Substituting this in the lever equation, we get:

\qquad \begin{align*} d_r &= \frac{L}{\frac{Fr}{Fe}}\\[1.5em] \implies d_r &= \frac{L}{MA} \end{align*}

Using this fulcrum equation, we can calculate lever distances for all class II levers.

For Class III levers, the length of the lever is:

\kern{4.3em} L = d_r

In other words, the fulcrum and the load are at the opposite ends of the lever. Substituting this in the lever equation, we get:

\qquad \begin{align*} d_e &= \frac{F_r}{F_e}L\\[1em] \implies d_e &= MA \cdot L \end{align*}

This fulcrum equation can calculate all lever distances for all class III levers.

Let's summarize everything we've learned so far in the next section.

How do you find the fulcrum point?

To calculate the fulcrum location of a lever of length L, follow these steps:

Determine the class of the lever based on the location of the fulcrum, the load F_r, and the effort F_e.
Calculate the mechanical advantage MA using the equation MA = F_r/F_e.
- For a class I lever, calculate the distance d_r of the fulcrum from the load using d_r = L / (MA + 1).
- For a class II lever, determine the distance d_r of the fulcrum from the load using d_r = L / MA.
- For a class III lever, the distance d_r of the fulcrum from the load is equal to the length of the lever, d_r = L.

How to use this lever fulcrum calculator

This fulcrum calculator will help you pinpoint the ideal fulcrum location for your lever, no matter the lever class. It is pretty simple to use:

Select the appropriate lever class from the Lever class list.
- Enter the correct values for the Load, Effort, and the Length of the lever fields. This calculator will show you the ideal fulcrum position relative to the load and effort and the mechanical advantage you will achieve.
- Alternatively, give the correct values for the Length of the lever and Mechanical advantage you want to achieve. You will get the best fulcrum position relative to the load and effort.

FAQs

Which fulcrum position on a 1m lever can give twice the mechanical advantage?

1/3 m away from the load and 2/3 m away from the effort.

To calculate the fulcrum position that gives a mechanical advantage of MA = 2 with a class I lever of length L = 1 m, follow these simple steps:

Calculate the distance d_r from the load to the fulcrum using d_r = L/( MA + 1) = 1/3.
Determine the distance d_e from the fulcrum to the effort using d_e = L - d_r = 1 - 1/3 = 2/3.
Verify your results using our fulcrum calculator.

What type of lever is the human elbow joint?

The human elbow joint is an example of a Class III lever. When we lift loads in our fists, the elbow joint acts as a fulcrum and the bicep muscle exerts the needed force a small distance from the elbow.

How do you calculate the length of the effort arm?

To calculate the length of the effort arm d_e of a lever to lift a load F_r with an effort F_e, follow these simple steps:

Determine the mechanical advantage MA using MA = F_r/F_e.
Measure the length of the load arm d_r as the distance between the fulcrum and the load.
Multiply MA with d_r to get the effort arm as d_e = MA × d_r.

Related calculators

VPD Calculator & Chart (Vapor Pressure Deficit)Sod Calculator Molar Mass Calculator Stone Weight Calculator Board and Batten Calculator