Force Calculator

The force calculator is here to help you calculate force from Newton's second law of motion. Read on to learn what force is and what types of forces are there in classical mechanics. We'll also explain how to find force in exercises using the force formula. At the end, we also illustrate what net force is with an easy example.

If you need to find a specific force, maybe one of these calculators can help you:

• Gravitational force calculator
• Normal force calculator
• Centrifugal force calculator
• Friction calculator
• Tension calculator
• Buoyancy calculator
• Pressure calculator

What is force?

If asked, "What is force?" a non-physicist would probably think about pushing and pulling. A physicist would think about the change in the velocity of an object. To understand why let's look at the force equation:

where:

• $\small a$ — Acceleration of the object expressed in metre per second squared $\small\rm [m/s^2]$;
• $\small m$ — Mass of an object in kilograms $\small \rm [kg]$; and
• $\small F$ — Force measured in Newtons $\small \rm [N]$.

Acceleration is the change of velocity over time. And, as you see from the force formula, the greater the force, the greater the acceleration. So, if something is speeding up, for example, a car, it can impart a significant force if it crashes into another car. This force is proportional to the car's mass and its (stopping) acceleration. Another example would be the human punch force, where the mass and acceleration of the body are directly proportional to the impact force.

To use the force calculator, input two of these variables: mass, acceleration, or force in any unit and get the missing number in the blink of an eye.

If you're calculating force on your own, always use the SI system to avoid mistakes. What is the SI unit of force? It's Newton $\footnotesize \bold{[N]}$ — named after Isaac Newton — mathematician, physicist, and discoverer of gravity. In SI base units, one Newton is equal to:

To learn more about force units, go to our force converter.

Newton came up with three laws of motion that explain the movement of all physical objects. They are the basics of all classical mechanics, which is also known as Newtonian mechanics.

1. Newton's first law of motion

   An object will remain at rest or continue to move in uniform motion unless acted upon by an external force.

2. Newton's second law of motion

   The force exerted by an object equals mass times acceleration of that object: $\small F = m \cdot a$.

3. Newton's third law of motion

   When one body exerts a force on a second body, the second body exerts a force equal in magnitude and opposite in direction on the first body (for every action, there is always an equal but opposite reaction).

All forces in classical mechanics are subject to three of Newton's laws of motion.

• Gravitational force is the attraction between any two objects of nonzero mass. You walk on the ground instead of floating because of this force — gravity. It's exerted by everything around you, like the screen you're reading this on. It's just so small; it's unnoticeable.

• Normal force is the reaction to gravitational force — a perfect example of Newton's third law. When you're standing, you exert a force (equal to gravitational force) on the floor. The floor exerts on you a force of the same value.

• Friction is a force that opposes motion. It's proportional to the normal force acting between an object and the ground. In winter, you apply sand on icy surfaces to increase friction and prevent slipping.

• Tension is an axial force that passes through ropes, chains, springs, and other objects when there is external pulling. For example, if you're walking your dog, and it pulls you forward, it creates tension on its leash.

• Centripetal force is a force acting on a rotating object. Have you ever been on a carousel? Do you remember the feeling of being pushed outwards? That feeling is called inertia (first Newton's law), and the centripetal force is what keeps you rotating.

• Pressure is the measure of the force applied on a surface. If you inflate a balloon, particles of air inside put pressure on the balloon. All particles feel the same force, so the balloon is inflated evenly.

Let's look at a few exercises so that nothing can surprise you in your physics class.

1. Find the accelerating and retarding (stopping) force:

A cheetah has a mass of 50 kg. It accelerates from rest to 50 km/h in 3 seconds. Then it starts steadily slowing down and stops after 8 seconds.

• Accelerating force:

  First, find acceleration:

  $\small 50 \space \text{km/h}$ is equal to $\small 13.89 \space \text{m/s}$ (we calculated this with the speed converter).

  Acceleration is equal to a difference in velocity over time:

Calculate accelerating force:

• Decelerating force:

Retarding force is negative because it has an opposite direction to the accelerating force.

2. How much force do you need to accelerate an object ($\small \bold{ m = 2 \space kg}$) by $\small \bold{8\ \rm{m/s^2}}$? What about when the object is three times heavier? How does it affect the force?

If the mass is three times heavier, the force needs to be three times bigger.

Force is a vector. It means that it has a value and direction. That's why you can't add it like regular numbers (scalars).

The net force ($\small F_{\text{N}}$) is the sum of the vectors of all individual forces acting on an object. For example, let's look at a falling ball. It is affected by the gravitational force ($\small F_{\text{G}} = 5\ \rm N$), air resistance ($\small F_{\rm R} = 1\ \rm N$), and lateral force caused by wind ($\small F_{\rm W} = 2\ \rm N$).

1. First, find the net force of vertical forces. They have opposite directions, so, in part, they cancel each other:

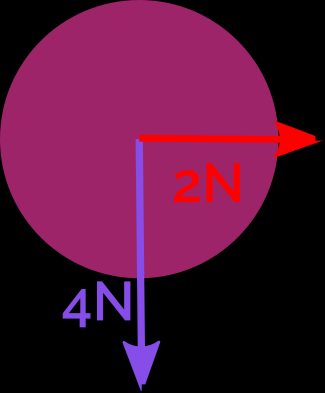
2. Now, find the net force of the two remaining forces.

   Here, you can calculate it using Pythagorean theorem (in a right triangle: $\small a^2 + b^2 = c^2$). To learn more about adding vectors, visit the vector addition calculator.

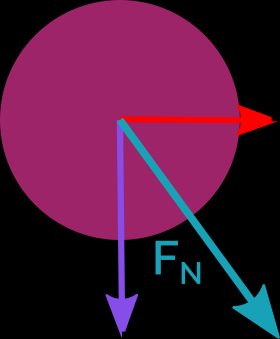
The net force acting on a ball equals 2√5 N.

Now that you know Newton's three laws of motion and force definition, look at one of the calculators listed at the beginning. We explain there in detail all types of forces. We also recently did a fun experiment where we tested what would win a race – a toilet roll or a bottle. Check it out to learn something about mass moment of inertia and acceleration!