Tension Calculator

This tension calculator will teach you how to find the tension force in a rope or string used to lift an object. In this article, you can also learn how to find tension in ropes used to pull an object on a frictionless surface. You will also see in this rope or string tension calculator a variety of free-body diagrams to further understand how to calculate tension forces. If you want to learn more about tension and the tension force formula, read on!

Imagine that you pick up a basketball from the ground. You would feel the ball's weight in your hands because of the force of gravity acting on the ball's mass. Now imagine tying a rope around the ball, which you then use to lift the ball again. You would still feel the ball's weight through the rope. In this situation, the rope is now in tension. What keeps the rope together is called the tension force. Cutting the rope will release the tension force and put the ball in free fall.

Tension force is an axial force that passes through an object that pulls, like a rope, string, or chain. We can also observe tension force in other materials, like rods and bars, given that they are subjected to external pulling or tensile loads. Materials with high tensile strength make the best rods and bars as they don't break easily when subjected to tension forces. You can check our stress calculator, which discusses elasticity, to learn more about tensile strength.

Tension force is also a great example of Newton's Third Law of Motion. Newton's Third Law of Motion states that when a body exerts a force on a second body, the second body exerts an equal force in the opposite direction back onto the original body. Tension force is a reactive force that counteracts an external pulling force.

To calculate the tension that acts in a rope, we first need to understand Newton's Second Law of Motion. Newton's Second Law of Motion states that the sum of the forces acting on an object of constant mass is equal to the mass of that object multiplied by its acceleration. We can also express this statement as an equation:

ΣF = m × a

where:

• Σ (sigma) denotes the summation of forces F;
• m is the mass of the object; and
• a is the acceleration.

For an object suspended by a rope, we can use acceleration due to gravity, g, as its acceleration. Gravitational acceleration gives us the value of its weight in terms of force, like in Newtons or pound-force. If the object is moving at a different acceleration, we should use its actual acceleration for the calculation. However, this tension calculator only determines the tension forces in cases of static equilibrium.

This statement means that this tool only considers objects at rest in a given system. In this tension calculator, we also assume that ropes are massless and, therefore, do not contribute anything to the tension forces. We also assume that the masses or objects are in a vacuum and do not experience friction or air resistance toward their surroundings.

We can see in the illustration below that the force, F, needed to lift the object is equal to the weight, W, of the object. This idea is the fundamental concept that underlies our tension force formula. Also shown below is the free-body diagram of the object, which shows the tension forces, T, acting in the string. As you can see, the tension forces come in pairs and in opposite directions:

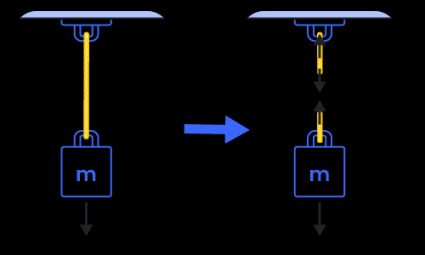
Following Newton's Second Law of Motion, we can then express the summation of forces using the free-body diagram of the object, as shown on the right side of the illustration above. We use free-body diagrams to show the different directions and magnitudes of the forces that act on a body. In equilibrium, these forces should all equate to zero. Considering all upward forces as positive and downwards as negative, our equation is:

ΣF↑ = 0 = T + (-W)

T = W

where weight, W, becomes negative since it is directed downwards. By transposing W to the other side of the equation, we can now see that the tension force in the rope is equal to the weight of the object it carries, as also shown above.

If we use more ropes to lift the object, the total tension force gets divided up into the ropes. The tension force in each rope depends on its angle with respect to the direction of the force it opposes. To further understand this, let us consider another free-body diagram of an object suspended by two ropes, as shown below:

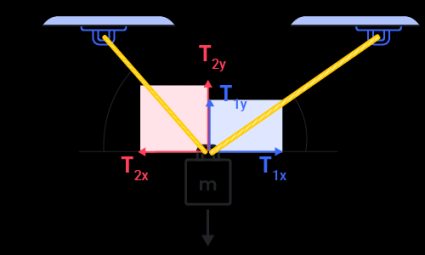
In the free-body diagram shown above, we can see the horizontal and vertical components of the tension forces, T₁, and T₂. Forces are vectors, which means they always have both magnitudes and directions. Like all vectors, forces can be expressed in these components, which give the force's influence along the horizontal and vertical axes. T₁ₓ and T₂ₓ are the horizontal components of T₁ and T₂, respectively. On the other hand, T_1y and T_2y are the vertical components of the same forces, respectively. Since gravity acts on the object in the vertical axis, we need to consider the tension forces' vertical components for our summation of forces as follows:

ΣF↑ = 0 = T_1y + T_2y + (-W)

W = T_1y + T_2y

Because we also know the angles of the tension forces, we can express T_1y and T_2y in terms of T₁ and T₂, respectively, with the help of trigonometric functions:

T_1y = T₁ × sin(α)

T_2y = T₂ × sin(β)

W = T₁ × sin(α) + T₂ × sin(β)

We can also say that for the system to be in equilibrium, the object should not move horizontally or along the x-axis. Therefore, the horizontal components of T₁ and T₂ must then equate to zero. Also, with the help of trigonometry, we can express T₁ₓ and T₂ₓ in terms of T₁ and T₂, respectively:

T₁ₓ = T₂ₓ

T₁ × cos(α) = T₂ × cos(β)

If we divide both sides by cos(α), we obtain an equation wherein T₁ is expressed in terms of T₂ and the angles:

T₁ = T₂ × cos(β) / cos(α)

We can then use this equation to solve for T₂ by substituting T₂ × cos(β) / cos(α) as the T₁ in our summation of forces equation, as shown below:

W = T₁ × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]

T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]

Finally, if we multiply this entire equation by cos(β) / cos(α) as we derived in the value of T₁ in terms of T₂, and then simplifying everything, we get this equation:

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(α) × sin(β) / cos(β) + sin(α)]

Now all you need to know are the angles of the tension ropes with respect to the horizontal. If an angle from the vertical is given, just subtract this angle from 90°. Doing so will provide you with the angle from the horizontal. However, if you are given other values of angles that may be greater than 90° or even 180°, you might want to check out our reference angle calculator to help you determine the angle you need. After determining the values for the variables in our tension force formulas, we can now solve for the tension forces.

How to find the tension force on an object being pulled is just like when the object is hung. The only difference is that we first need to compute the acceleration of the entire system and sum all of the of forces along the horizontal. If the rope is at an angle from the level of the floor, we need to compute for the horizontal component of the pulling force too.

Let us take a look at the example below to better understand how to find the tension force in a rope pulling one or two objects. In this example, two objects are being pulled by a single applied pulling force. Another rope is pulling the second object, which is attached to the first object, as shown below:

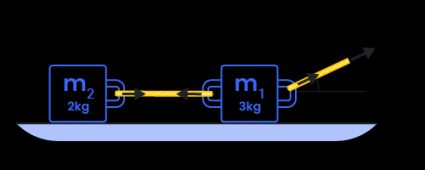
This illustration shows that the masses of m₁ and m₂ are 3 kg and 2 kg, respectively. The sum of these two masses gives the total mass of the system, 5 kg. We also need to determine the horizontal component of the pulling force, T = 24 N, that is at an angle θ = 60°. If we use the trigonometric functions again, we can say that the horizontal component of the pulling force is equal to 24 N × cos(60°), which is equal to 12 N. Now that we know the pulling force's horizontal component and the total mass of the system, we can now calculate the acceleration, a, of the system as follows:

F = m × a → a = F / m

a = 12 N / 5 kg = 2.4 m/s²

After we have found the acceleration of the system, we can use Newton's Second Law of Motion again to calculate the system's rope or string tension. To do this, multiply the acceleration by the mass that the rope is pulling. For T₂, its free-body diagram shows us it is only responsible for the mass of m₂; we can say that T₂ = a × m₂. With that said, T₂ = (2.4 m/s²) × (2 kg) = 4.8 N. On the other hand, T₁ is the tension force that pulls both the weight of m₁ and m₂. However, we already have the value for T₁, which is simply equal to T = 24.0 N. Therefore, T₁ = 24.0 N.

In our example, if the left and right ropes were just a single rope, we could compare this setup to a pulley system. A pulley is a simple machine that takes advantage of tension forces in ropes to gain mechanical advantage. You can check out our pulley calculator and belt length calculator (which is a two-pulley system) to learn more about mechanical advantage and tension.