Acceleration Calculator

Our acceleration calculator is a tool that helps you to find out how fast the speed of an object is changing. It works in three different ways, based on:

1. Difference between velocities at two distinct points in time.
2. Distance traveled during acceleration.
3. The mass of an accelerating object and the force that acts on it.

If you're asking yourself what is acceleration, what is the acceleration formula, or what are the units of acceleration, keep reading, and you'll learn how to find acceleration. Acceleration is strictly related to the motion of an object, and every moving object possesses specific energy.

To keep things clear, we also prepared some acceleration examples that are common in physics. You can find there:

1. Centripetal acceleration and tangential acceleration.
2. Angular acceleration.
3. Acceleration due to gravity.
4. Particle accelerator.

Acceleration always occurs whenever there is a non-zero net force acting on an object. You can feel it in an elevator when you become a little heavier (accelerating) or lighter (decelerating) or when you're riding down a steep slope on your sled in the snow. What's more, from the general theory of relativity, we know that the entire Universe is not only expanding, but it is even an accelerated expansion! That means that the distance between two points is constantly becoming greater and greater, but we can't feel that on an everyday basis because every scale in the world expands too.

Acceleration is the rate of change of an object's speed; in other words, it's how fast velocity changes. According to Newton's second law, acceleration is directly proportional to the summation of all forces that act on an object and inversely proportional to its mass. It's all common sense – if several different forces are pushing an object, you need to work out what they add up to (they may be working in different directions) and then divide the resulting net force by your object's mass.

This acceleration definition says that acceleration and force are, in fact, the same thing. When the force changes, acceleration changes too, but the magnitude of its change depends on the mass of an object (see our magnitude of acceleration calculator for more details). This is not true in a situation when the mass also changes, e.g., in rocket thrust, where burnt propellants exit from the rocket's nozzle. See our rocket thrust calculator to learn more.

We can measure acceleration experienced by an object directly with an accelerometer. If you hang an object on the accelerometer, it will show a non-zero value. Why is that? Well, it's because of gravitational forces that act on every particle that has mass. And where is a net force, there is an acceleration. An accelerometer at rest thus measures the acceleration of gravity, which on the Earth's surface is about 31.17405 ft/s² (9.80665 m/s²). In other words, this is the acceleration due to gravity that any object gains in free fall when in a vacuum.

Speaking of vacuums, have you ever watched Star Wars or another movie that takes place in space? The epic battles of spaceships, the sounds of blasters, engines, and explosions. Well, it's a lie. Space is a vacuum, and no sound can be heard there (sound waves require matter to propagate). Those battles should be soundless! In space, no one can hear you scream.

The acceleration calculator on this site considers only a situation in which an object has a uniform (constant) acceleration. In that case, the acceleration equation is, by definition, the ratio of the change in velocity over a particular time.

Here, you can learn how to find acceleration in two more ways. Let's see how to use our calculator (you can find acceleration equations in the section after):

• Depending on what data you have, you may calculate acceleration in three different ways. First of all, select an appropriate option at the top ("Speed difference", "Distance traveled" or "Mass and force").

• For speed difference — Enter the initial v_i and final v_f speeds of the object and how much time Δt it took for the speed to change (see our speed calculator if required).

• For distance traveled — Enter initial speed v_i, distance traveled Δd and time Δt passed during acceleration. Here, you don't need to know the final speed.

• For mass and force — Enter the mass m of the object and the net force F acting on this object. This is an entirely different set of variables that arises from Newton's second law of motion (another definition of acceleration).

• Read the resulting acceleration from the last field. You can also perform calculations in the other way if you know what acceleration is, for example, to estimate distance Δd. Just provide the rest of the parameters in this window.

In the 17th century, Sir Isaac Newton, one of the most influential scientists of all time, published his famous book Principia. In it, he formulated the law of universal gravitation, which states that any two objects with mass will attract each other with a force exponentially dependent on the distance between these objects (specifically, it is inversely proportional to the distance squared). The heavier the objects are, the greater the gravitational force. It explains, for example, why planets orbit around the very dense Sun.

In Principia, Newton also includes three laws of motion which are central to understanding the physics of our world. The acceleration calculator is based on three various acceleration equations, where the third is derived from Newton's work:

1. a = (v_f − v_i) / Δt;
2. a = 2 × (Δd − v_i × Δt) / Δt²; and
3. a = F / m.

where:

• a — Acceleration;
• v_i and v_f are, respectively, the initial and final velocities;
• Δt — Acceleration time;
• Δd — Distance traveled during acceleration;
• F — Net force acting on an object that accelerates; and
• m — Mass of this object.

Now you know how to calculate acceleration! In the next paragraph, we discuss the units of acceleration (SI and Imperial).

If you already know how to calculate acceleration, let's focus on the units of acceleration. You can derive them from the equations we listed above. All you need to know is that speed is expressed in feet per second (imperial/US system) or in meters per second (SI system) and time in seconds. Therefore, if you divide the speed by time (as we do in the first acceleration formula), you'll get acceleration unit ft/s² or m/s² depending on which system you use.

Alternatively, you can use the third equation. In this case, you need to divide force (poundals in US and newtons in SI) by mass (pounds in US and kilograms in SI), obtaining pdl/lb or N/kg. They both represent the same thing, as poundal is pdl = lb·ft/s² and the newton is N = kg·m/s². When you substitute it and reduce the units, you'll get (lb·ft/s²) / lb = ft/s² or (kg·m/s²) / kg = m/s².

There is also a third option that is, in fact, widely used. You can express acceleration by standard acceleration due to gravity near the surface of the Earth, which is defined as g = 31.17405 ft/s² = 9.80665 m/s². For example, if you say that an elevator is moving upwards with the acceleration of 0.2g, it means that it accelerates with about 6.2 ft/s² or 2 m/s² (i.e., 0.2 × g). We rounded the above expressions to two significant figures.

Centripetal acceleration and tangential acceleration

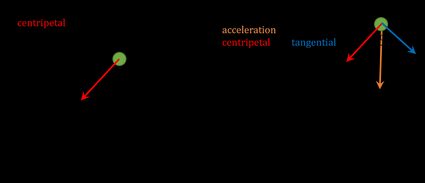
Acceleration is generally a vector, so you can always decompose it into components. Usually, we have two parts that are perpendicular to each other: the centripetal and the tangential. Centripetal acceleration changes the direction of the velocity, and therefore the shape of the track, but doesn't affect the value of the velocity. On the other hand, tangential acceleration is always parallel to the trajectory of motion. It changes the value of velocity only, and not its direction.

In a circular motion (the leftmost picture below), where an object moves around the circumference of a circle, there is only the centripetal component. An object will keep its speed at a constant value; think of the Earth, which has centripetal acceleration due to the gravity of the Sun (in fact, its speed changes a bit during a year).

When both components are present, the object's trajectory looks like the right picture. What happens if there is only tangential acceleration? Then linear motion occurs. This is similar to when you press down on the gas pedal in a car on a straight part of the freeway.

Angular acceleration

Angular acceleration plays a vital role in the description of rotational motion. However, don't confuse it with the previously mentioned centripetal or tangential accelerations. This physical quantity corresponds to the rate of change of angular velocity. In other words, it tells you how fast an object's rotations accelerate – the object spins faster and faster (or slower and slower if angular acceleration is less than zero). Check out our angular acceleration calculator for more information.

Did you know that we can find an analogy between this and Newton's law of dynamics in rotational motion? In his second law, if you can switch acceleration with angular acceleration, force with torque, and mass with moment of inertia, you'll end up with the angular acceleration equation. You might notice that some physical laws, like this one, are universal, which makes them really important in physics.

Gravitational acceleration

We mentioned acceleration due to gravity a few times earlier. It arises from the gravitational force that exists between every two objects that have mass (note that the gravity equation isn't dependent on an object's volume – only mass is essential here). It may sound weird at first, but according to the third Newton's law of motion, you act with the same force on the Earth as the Earth acts on you. However, the mass of the Earth is much bigger than a human mass (~10²² times bigger), so our impact on the Earth is pretty much zero. It's analogous to all the bacteria (~10¹⁸ times lighter than a human) living on your hand; you can't even notice them! On the other hand, we can feel the influence of our planet, and that's the acceleration due to gravity.

Standard gravity is, by definition, 31.17405 ft/s² (9.80665 m/s²), so if a human weighs 220 lb (about 100 kg), he is subjected to the gravitational force of about 7000 pdl (1000 N). Let's enter this value into window #3 of our calculator along with the mass of the Earth (1.317 × 10²⁵ lbs or 5.972 × 10²⁴ kg in scientific notation). What is the calculated acceleration? It is so small that our calculator considers it to be zero. We mean nothing compared to the planet!

Particle accelerator

After talking about huge objects in space, let's move to the microscopic world of particles. Although we can't see them with our eyes, we have harnessed high-energy particles, like electrons and protons, and use them regularly in particle accelerators, common in physics, chemistry, and medicine. We use them to kill cancer cells while sparing the surrounding healthy tissue or investigate a material's structure at the atomic scale. Recently, cancer is one of the diseases of affluence that probably result from the increasing wealth in society.

You probably know about the Large Hadron Collider (CERN), the most powerful particle accelerator in the world. It allows us to take a step further to understand how the universe works and develop technologies that may have many essential applications in the future. However, to achieve such high energies, we have to accelerate particles to speeds that are close to the speed of light. Briefly, we can do it using magnetic or electric fields.